Replicating AlphaGo

Tags: #Reinforcement Learning #Go
Last updated: 01 Mar 2024

Contents

A Little bit of History

Generated using Google Gemini

Codes

You can find the codes for the following article from the Github

Go, also known as Baduk in Korea, has a long history spanning over 2500 years and is loved by many in East Asia. In this game, players take turns placing black and white stones on a grid, aiming to control territory and capture their opponent's stones. The game gets more complicated as the board size increases, but typically, players use boards with 9, 13, or 19 squares.

In 2016, DeepMind, now Google DeepMind, made waves when AlphaGo defeated the legendary Lee Sedol. What made AlphaGo special was its use of advanced technology like deep neural networks and reinforcement learning, along with smart algorithms like Monte Carlo Tree Search (MCTS). By training on lots of Go data and playing millions of games against itself, AlphaGo learned to evaluate board positions and make strategic decisions really well.

I'm someone who plays Go and really enjoys it, even though I'm not that good at it. That was the main motivation for me to try replicating AlphaGo. Despite searching through many blogs and videos, I couldn't find what I needed. So, I decided to document my journey as I try to replicate AlphaGo, but for a 9x9 board.

Creating an Enviroment

Environment for this is heavily inspired by the repository Deep Learning and the Game of Go. Some changes have been made to the original code to make it more readable and understandable. Regardless of that, the original code contains more information and is much more detailed. It is a part of the book "Deep Learning and the Game of Go" by Max Pumperla and Kevin Ferguson. In this article, we are only focusing on the bare minimum to train an AlphaGo on a 9x9 board. The codes for the environment could be found in the alphago/env folder. If you are planning to code along, create a folder alphago and copy the env folder from the repository to the alphago folder. Initially I thought of just directly going to the codes of AlphaGo, but then later I thought it would be better to include many details like MCTS, neural networks, etc. separately. That way it would be easier for a beginner to understand the code. I would highly recommend going through the book Deep Learning and the Game of Go. It's a great book with a lot of information for beginners while this blog assumes you are already familiar with the basics of Go and PyTorch, deep learning.

Quick overview of enviroment

Files in env folder

env/
  - generate_zobrist.py
  - go_board.py
  - gotypes.py
  - scoring.py
  - utils.py
  - zobrist.py

generate_zobrist.py This file is used to generate Zobrist hash for the board. Run this file and copy output to zobrist.py, or python3 generate_zobrist.py > zobrist.py from the alphago/env directory.
go_board.py This file contains the GoBoard class which is our environment.
zobrist.py This file contains the Zobrist hash for the board which is generated using generate_zobrist.py.

Creating game state

Use the following snippet to create a 9x9 board.

>>> from alphago.env import go_board
>>> from alphago.env.utils import print_board, print_move

>>> board_size = 9
>>> game = go_board.GameState.new_game(board_size=board_size)

Rendering board

>>> print_board(game.board)
9  .  .  .  .  .  .  .  .  . 
8  .  .  .  .  .  .  .  .  . 
7  .  .  .  .  .  .  .  .  . 
6  .  .  .  .  .  .  .  .  . 
5  .  .  .  .  .  .  .  .  . 
4  .  .  .  .  .  .  .  .  . 
3  .  .  .  .  .  .  .  .  . 
2  .  .  .  .  .  .  .  .  . 
1  .  .  .  .  .  .  .  .  . 
   A  B  C  D  E  F  G  H  I

Taking actions

Movements are achieved using alphago.env.go_board.Move object. There are 3 types of movements available: play(point), pass(), and resign(). To apply the movement, you can use the apply_move method from the game object.

        >>> from alphago.env.go_board import Move
>>> from alphago.env.gotypes import Point
>>> point = Point(row=3,col=4)
>>> move = Move.play(point)
>>> # You can also do Move.pass() or Move.resign()
>>> print_move(game.next_player, move)
Player.black D3
>>> game = game.apply_move(move)
>>> print_board(game.board)
  9  .  .  .  .  .  .  .  .  . 
  8  .  .  .  .  .  .  .  .  . 
  7  .  .  .  .  .  .  .  .  . 
  6  .  .  .  .  .  .  .  .  . 
  5  .  .  .  .  .  .  .  .  . 
  4  .  .  .  .  .  .  .  .  . 
  3  .  .  .  x  .  .  .  .  . 
  2  .  .  .  .  .  .  .  .  . 
  1  .  .  .  .  .  .  .  .  . 
     A  B  C  D  E  F  G  H  I

Interacting with the Enviroment

Lets create our first agent to play Go. Before we move on to any greedy, or any intelligent approach, lets start with a random agent and see how it performs. We will use the following interface for all of our agents.

class Agent:
    def __init__(self):
        pass

    def select_move(self, game_state):
        raise NotImplementedError()

Random Agent

Now that we know how to use the environment, let's create a random bot for playing the game. We'll achieve this by overriding the select_move function, where we'll locate all valid movements and randomly select one from them. For people who are new to go, In Go. an eye is an empty space surrounded by stones of one color. If you fill in these spaces yourself, you make it easier for your opponent to surround you and capture your entire group, including the stones you just placed to fill those eyes. To check if a point is an eye, you can use the following code.

def is_point_an_eye(board, point, color):
    if board.get(point) is not None:
        return False
    for neighbor in board.neighbors(point):
        neighbor_color = board.get(neighbor)
        if neighbor_color != color:
            return False

    friendly_corners = 0
    off_board_corners = 0
    corners = [
        Point(point.row - 1, point.col - 1),
        Point(point.row - 1, point.col + 1),
        Point(point.row + 1, point.col - 1),
        Point(point.row + 1, point.col + 1),
    ]
    for corner in corners:
        if board.is_on_grid(corner):
            corner_color = board.get(corner)
            if corner_color == color:
                friendly_corners += 1
        else:
            off_board_corners += 1
    if off_board_corners > 0:
        return off_board_corners + friendly_corners == 4
    return friendly_corners >= 3

Now combining all what we have to create out first agent who can play go.

...
def select_move(self, game_state):
    candidates = []
    for r in range(1, game_state.board.num_rows + 1):
        for c in range(1, game_state.board.num_cols + 1):
            candidate = go_board.Move.play(Point(row=r, col=c))
            if game_state.is_valid_move(
              candidate
            ) and not is_point_an_eye(
              game_state.board, candidate, game_state.next_player
            ):
                candidates.append(candidate)
    return random.choice(candidates)

There is also a way to greatly speed up the random agent. We can cache the movements and randomly select one instead of iterating throught all the points and then randomly choosing one. The implementation for this FastRandomBot can be found in alphago/agents folder.

Agent-vs-Agent

I have implemented a simple human interfact as an agent. For more details you can refer to alphago/agents/human_agent.py The following code is a simple snippet for an agent vs agent game.

bots = {
  gotypes.Player.black: agents.RandomBot(),
  gotypes.Player.white: agents.HumanAgent(),
}

while not game.is_over():
  print_board(game.board)
  bot_move = bots[game.next_player].select_move(game)
  print_move(game.next_player, bot_move)
  game = game.apply_move(bot_move)

Tree Search - MCTS

We've figured out how to handle tic-tac-toe or a 5x5 Go board with our computer, which only has a few hundred thousand possible situations. But what about games like Go or chess? They've got more situations than all the atoms on Earth! So, we're using something called Monte Carlo Tree Search (MCTS) to figure out the game state without any fancy strategies. The idea's pretty simple: we're just randomly looking around to see how good a situation is. We build a tree with all the possible moves we can make from a given situation. But then again, we can't make a tree with every single situation because there are just way too many of them for our systems to handle.

So, MCTS basically has four parts:

Selection
Expansion
Simulation
Backpropagation

Let's break down every step in this.

Selection

Starting from the root node, we select the child node with the highest UCT (Upper Confidence Bound 1 applied to trees) value. The UCT value is calculated as follows:

$$UCT = \frac{Q}{N} + c \sqrt{\frac{\log{P}}{N}}$$

Where:

$\Large Q$ is the number of wins after the move.
$\Large N$ is the number of simulations after the move.
$\Large P$ is the number of simulations after the parent node.
$\Large c$ is the exploration parameter.

The first part of the equation is the exploitation term, and the second part is the exploration term. The exploration parameter is a hyperparameter that controls the balance between exploration and exploitation. A higher value of $c$ will lead to more exploration, and a lower value will lead to more exploitation. The reason why we need to explore is simple: The agent has to exploit what it has already experienced in order to obtain a reward, but it also has to explore in order to make better action selections in the future. (Reinforcement Learning - An Introduction by Richard S. Sutton and Andrew G., Chapter 1)

The implementation is as follows:

def select_child(self, node):
    """
    Selection
    """
    total_rollouts = sum(child.num_rollouts for child in node.children)
    log_total_rollouts = math.log(total_rollouts)

    best_score = -1
    best_child = None
    for child in node.children:
        win_pct = child.winning_pct(node.game_state.next_player)
        exploration_factor = math.sqrt(
          log_total_rollouts / child.num_rollouts
          )
        uct_score = win_pct + self.temperature * exploration_factor
        if uct_score > best_score:
            best_score = uct_score
            best_child = child
    return best_child

Expansion

Once we have selected a node, we need to expand it. We will add a new node to the tree at random. This is also called rollout.

Simulation

Once we have expanded the node, we will simulate the game from that node until the end and see who wins. It's to evaluate the current state of the game.

Backpropagation

Once we have the result of the simulation, we will update the nodes on the path from the root to the selected node. We will update the number of wins and the number of visits to each node.

MCTS Implementation

class MCTSNode:
  def __init__(self, game_state, parent=None, move=None):
      self.game_state = game_state
      self.parent = parent
      self.move = move
      self.children = []
      self.num_rollouts = 0
      self.unvisited_moves = game_state.get_legal_moves()
      self.win_counts = {
          Player.black: 0,
          Player.white: 0,
      }

  def add_random_child(self):
      index = random.randint(0, len(self.unvisited_moves) - 1)
      new_move = self.unvisited_moves.pop(index)
      next_state = self.game_state.apply_move(new_move)
      child = MCTSNode(next_state, self, new_move)
      self.children.append(child)
      return child

  def fully_expanded(self):
      return len(self.unvisited_moves) == 0

  def is_terminal(self):
      return self.game_state.is_over()

  def winning_pct(self, player):
      return float(self.win_counts[player]) / float(self.num_rollouts)

Next, we define a new Agent which uses this data structure and MCTS algorithm to play Go. We will now need to define select_move and for that, we will need to implement these methods to our agent:

Selection
Expansion
Simulation
Backpropagation

I have already discussed the first one, and the rest are relatively easy once you have an idea of how MCTS works. The complete implementation of the MCTS agent can be found in alphago/agents/mcts_agent.py file.

Bringing Neural Networks

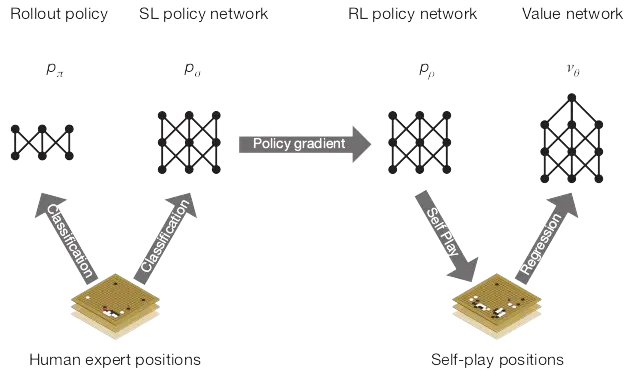
In the original paper, we train 4 different neural networks:

Rollout Policy, $p_\pi$
SL Policy Network, $p_\sigma$
RL Policy Network, $p_\rho$
Value Network, $v_\theta$

First, we have a fast rollout policy, which is a smaller network compared to the rest, and we actually use it in tree search for speed. In our case, since the board is 9x9, I won't be training a separate rollout policy network, but you are free to train it, and for that purpose, you can use the GoNet in alphago/networks. Next we have the supervised learning policy (SL) network that uses data from game plays to train the network. Then, we improve this network by playing against itself using reinforcement learning. Lastly, we have a value network that predicts the outcome of moves for the sake of strategic decision-making. Now lets start from the zero to train an alphago.

Before anything, the first thing we need to worry about is the data. We have two ways to obtain data in our case. The first step is to generate data using an MCTS agent. For that, we can define two MCTS agents and make them play against each other. We can also use random agents, but the quality of the game wouldn't be really good. But the thing is, we cannot just directly use the raw data that we obtain from playing with the MCTS agent. So what we can do is to convert these boards to an array where 0 represents empty space, -1 represents black stones, and 1 represents white stones. And for actions which are currently in the format (row, col), we can ravel them using the equation index = i * n + j. For this, we can define an encoder which can encode both the states and actions to something that neural networks can understand.

Encoder

Here we will implement a simple one-plane encoder. We will be using a 1x9x9 matrix to represent the board. In this matrix, 0 represents empty points, 1 represents the points occupied by the current player, and -1 represents the points occupied by the opponent. I won't be going into any detailed explanation of the implementation since it is pretty straightforward. The encoder is implemented in alphago/encoders/oneplane.py file. The following functions are relatively important in the encoder.

Encoding the board

def encode(self, game_state):
    board_matrix = np.zeros(self.shape())
    next_player = game_state.next_player
    for r in range(self.board_height):
        for c in range(self.board_width):
            p = Point(row=r + 1, col=c + 1)
            go_string = game_state.board.get_go_string(p)
            if go_string is None:
                continue
            if go_string.color == next_player:
                board_matrix[0, r, c] = 1
            else:
                board_matrix[0, r, c] = -1
    return board_matrix

Encoding the point

def encode_point(self, point):
    return self.board_width * (point.row - 1) + (point.col - 1)

Decoding the point index

def decode_point_index(self, index):
    row = index // self.board_width
    col = index % self.board_width
    return Point(row=row + 1, col=col + 1)

Even though there are different encoders we can try, I won't be discussing them because the current one we have works perfectly for 9x9 boards. In case you want to try creating one, please refer to the Extra Notes.

Generating Data

Now that we have our encoder, we can start generating data for our neural network. We will use the MCTS agent to generate data for us. We will play a game with the MCTS agent and store the encoded board state and the move made by the MCTS agent. We will then use this data to train our neural network. You can find the implementation of the data generation in archives/generate_mcts_game.py file. Additionally, I have rewritten the code, which now uses multiprocessing to play multiple games at the same time. You can find that in archives/generate_mcts_game_mp.py file.
But don't you think this is actually troublesome because it will take us a lot of time to get enough data, and also we can obtain data of games which are equal or better in terms of quality from real-world Go games? So when you think about factors like that, the best option we have right now is to download the datasets which were already created by other people, and most of them are the game records of top amateur games played on competitions or servers like OGS. Here are some of the links to the datasets:

K Go Server amateur 19x19
K Go Server 4Dan 19x19
cwi.nl contains a huge collection of go games
Juno contains some datasets hosted by me.

All of these datasets are in SGF format and we need to convert them to tensors for us to train the neural networks. I have implemented a dataset which is compatible with PyTorch DataLoader in alphago/data folder. The idea behind this implementation is simple:

Download the dataset, if not present
Sample X amount of games (i.e X sgf files)
Save each board state and movement to the dataset (use multiprocessing)

[Note]:If you have your own dataset, paste the folder containing sgf files into your dataset folder and pass name of the folder to the dataloader.

This is how you use the GoDataSet.

from alphago.data.dataset import GoDataSet

BOARD_SIZE = 9
print(GoDataSet.list_all_datasets()) #prints all available datasets
training_dataset = GoDataSet(
  encoder = "oneplane", # encoder used
  game = "go9", # Dataset name, 
  no_of_games = 8000, # number of games
  dataset_dir="dataset", # directory
  seed = 100,
  redownload = False,
  avoid = [] # files to avoid
)
test_dataset = GoDataSet(
  encoder="oneplane", no_of_games=100, avoid=training_dataset.games
)
train_loader = torch.utils.data.DataLoader(
    training_dataset, batch_size=64, shuffle=True
)

Simple supervised Learning

Let's start by defining the neural network which trains on the Go9 dataset.

class AlphaGoNet(nn.Module):
  def __init__(self, input_shape, num_filters=192, dropout=0.3):
      super(AlphaGoNet, self).__init__()
      self.input_shape, self.num_filters, self.dropout = input_shape, num_filters, dropout
      self.conv1 = nn.Conv2d(input_shape[0], num_filters, 3, 1, 1)
      self.conv2 = nn.Conv2d(num_filters, num_filters, 3, 1, 1)
      self.conv3 = nn.Conv2d(num_filters, num_filters, 3, 1)
      self.conv4 = nn.Conv2d(num_filters, num_filters, 3, 1)
      self.bn1, self.bn2, self.bn3, self.bn4 = *[
        nn.BatchNorm2d(num_filters) for _ in range(4)
      ]
      self.fc1 = nn.Linear(num_filters * (
        (input_shape[1] - 4) * (input_shape[2] - 4)), 1024)
      self.fc_bn1 = nn.BatchNorm1d(1024)
      self.fc2 = nn.Linear(1024, 512)
      self.fc_bn2 = nn.BatchNorm1d(512)
      self.fc3 = nn.Linear(512, input_shape[1] * input_shape[2])
      self.fc4 = nn.Linear(512, 1)

  def forward(self, s):
      s = F.relu(self.bn1(self.conv1(s.view(-1, 1, self.input_shape[1], self.input_shape[2]))))
      s = F.relu(self.bn2(self.conv2(s)))
      s = F.relu(self.bn3(self.conv3(s)))
      s = F.relu(self.bn4(self.conv4(s)))
      s = s.view(-1, self.num_filters * ((self.input_shape[1] - 4) * (self.input_shape[2] - 4))))
      s = F.dropout(F.relu(self.fc_bn1(self.fc1(s))), p=self.dropout, training=self.training)
      s = F.dropout(F.relu(self.fc_bn2(self.fc2(s))), p=self.dropout, training=self.training)
      pi, v = self.fc3(s), self.fc4(s)
      if self.training:
          return F.log_softmax(pi, dim=1), torch.tanh(v)
      return F.softmax(pi, dim=1), torch.tanh(v)

Now that we have a model, we can just go ahead and train it as you would with a normal deep learning model. You can use torch.nn.functional.nll_loss or torch.nn.CrossEntropyLoss. If you are going to use the latter, then please one-hot encode the labels before feeding them to the neural network. Code for the training can be found in alphago_sl.py.

I have also trained this with the 19x19 KGS dataset, but the results weren't that great. Of course, it's better than a random agent, but that doesn't mean it's good enough to win a real-world game, let alone a beginner-level game. Maybe training on more data and increasing epochs might do the trick, but it won't be enough to defeat an average Go player. The only reason our 9x9 model is performing well at this point is because of its lower complexity compared to larger boards. But then again, I wouldn't go as far as to say our model is good enough to defeat an intermediate Go player. Why? It seems like something is missing, isn't it? As an answer to this, I say experience. When we think about how we humans are different from these deep learning or any machine learning models, we might have a lot of answers, but the most relevant and important one would be our ability to learn from experience. And how do we gain experience? The answer is simple: we humans spend a lot of time practicing, training, and improving upon our knowledge. Likewise, we introduce the concept of learning from experience, the concept of practice, to computers by using reinforcement learning. The next section will be about how we can use reinforcement learning to improve our model by practicing, also known as self-play.

[Note]: We are supposed to train the fast rollout policy network, but I won't be doing that and instead will be using the supervised model as the fast rollout policy. However, as I explained before, you can feel free to train the fast rollout if you want to.

Reinforcement Learning

I won't be explaining much about reinforcement learning in this article since it won't fit within this limited space, and our main objective here is to teach an agent to play Go. However, I will provide a brief overview of reinforcement learning. Reinforcement learning is very similar to how we humans learn. We are rewarded when we perform well and punished when we make mistakes. In reinforcement learning, the focus is on learning optimal behavior to maximize rewards.

If you're interested in learning more about reinforcement learning, you can explore the following resources:

Reinforcement Learning: An Introduction Andrew Barto and Richard S. Sutton
UCL Course on RL David Silver

These will provide you with more comprehensive insights into the topic.

Back to our topic, we know that experience is very important for a human to take action. For animals, we have brains to store these experiences. But what about our agents? It's not like our agents have a brain already integrated into them. To address this, we create a small data structure which stores the relevant information we need. In our case, we store the state of the board, the action we took, and the reward we received. Now that we have a brain, don't we need to fill our brains with some relevant data? So, we do something called self-play where an agent plays against another. Collecting experience by playing with a random agent isn't a great idea since the gathered data isn't great. We can use MCTS, but it would take a huge amount of time since you will need records of a lot of games, probably around 10,000 or more. Then we can do an agent vs. human, but that would take an eternity, lol. So, we play against the supervised learning model against itself. Essentially, what happens is self-play of two instances of the deep learning agent we trained earlier. By the end, we will discuss the training of the last two networks we need for AlphaGo, the Policy network and the Value network.

Training the Policy Network

In the original paper, they used the supervised model and improved it using self-play, and this is what we should do. So here, for us to improve the model, the idea is simple: we take the supervised model, do a lot of self-play, around 10,000 games would be fine but remember more is better, and store those data. Since I won't be explaining the complete codes, I will explain how the data would be like. So, say you won a game in self-play; in that case, for all states and all the actions we encountered and took, we store a +1 reward, and for the states and actions which we lost the game, we store a -1 reward. And now you can go ahead and train the policy network like how you would do for a normal neural network. Codes for the self-play and training can be found in alphago_rl.py.

Training the Value Network

Now we need a value network to evaluate the board position. We can use the policy model which we trained in the last section for training our value network. In the last case, we considered both the state and action to get the y value which is the reward. In this case, since we are only evaluating how good a position is, we will only need the state. If the state in self-play resulted in a win then we consider the target label for that as +1 else we give 0. Codes for the training can be found in alphago_value.py.

AlphaGo

Now let's bring together all that we have. In the beginning, we trained two policy networks, one of which is small and the other one is comparatively large. The smaller, faster policy network is used in tree search rollouts, while the larger one is optimized for accuracy. After supervised learning, we engage in self-play to improve this network and make it stronger. In our case, we won't be training a different fast rollout network; instead, we'll use the supervised model. With the data from self-play by the policy network, we train a value network, which is an essential part of AlphaGo.

Neural Networks in MCTS

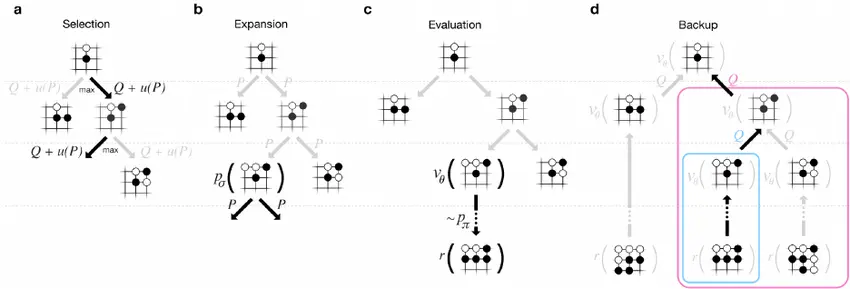
AlphaGo uses a more complex tree search than the one we used before, but the 4 parts of classic MCTS are still relevant to AlphaGo's MCTS. The only difference is that we are using a deep learning network to evaluate positions and nodes. Let's start with the rollout.

def policy_rollout(self, game_state):
  for step in range(self.rollout_limit):
      if game_state.is_over():
          break
      move_probabilities = self.rollout_policy.predict(game_state)[0]
      encoder = self.rollout_policy.encoder
      for idx in np.argsort(move_probabilities)[::-1]:
          max_point = encoder.decode_point_index(idx)
          greedy_move = Move(max_point)
          if greedy_move in game_state.legal_moves():
              game_state = game_state.apply_move(greedy_move)
              break

  next_player = game_state.next_player
  winner = game_state.winner()

  if winner is not None:
      return 1 if winner == next_player else -1
  else:
      return 0

This is pretty much the same as our rollout in classic MCTS. However, as you can see, there is a rollout_limit in place to avoid the rollout taking up a huge amount of time. Then, we have a policy_probabilities function to compute the policy values for the legal moves available to us.

def policy_probabilities(self, game_state):
  encoder = self.policy.encoder
  outputs = self.policy.predict(game_state)[0]
  legal_moves = game_state.legal_moves()
  if len(legal_moves) == 2:
      return legal_moves, [1, 0]
  encoded_points = [
      encoder.encode_point(move.point) for move in legal_moves if move.point
  ]
  legal_outputs = outputs[encoded_points]
  normalized_outputs = legal_outputs / np.sum(legal_outputs)
  return legal_moves, normalized_outputs

Next we have our most important function, select_move.

def select_move(self, game_state):
  for sim in range(self.num_simulations):
      current_state = game_state
      node = self.root
      for depth in range(self.depth):
          if not node.children:
              if current_state.is_over():
                  break
              moves, probabilities = self.policy_probabilities(current_state)
              node.expand_children(moves, probabilities)
          move, node = node.select_child()
          current_state = current_state.apply_move(move)
      value = self.value.predict(current_state)
      rollout = self.policy_rollout(current_state)

      weighted_value = (
          1 - self.lambda_value
      ) * value + self.lambda_value * rollout

      node.update_values(weighted_value)

  moves = sorted(
      self.root.children,
      key=lambda move: self.root.children.get(move).visit_count,
      reverse=True,
  )

  for i in moves:
      if not is_point_an_eye(
        game_state.board, i.point, game_state.next_player
      ):
          move = i
          break
  else:
      move = Move.pass_turn()
  self.root = AlphaGoNode()
  if move in self.root.children:
      self.root = self.root.children[move]
      self.root.parent = None
  return move

The idea of select_move is simple: we play a number of simulations. We restrict the game length using depth, so we play until the specified depth is reached. If we don't have any children, we expand them using the probabilities of moves from the strong policy network. Note that the policy network returns all the moves and their associated probabilities. We update this information to the AlphaGo Node using the following function in the Node.

def expand_children(self, moves, probabilities):
    for move, prob in zip(moves, probabilities):
        if move not in self.children:
            self.children[move] = AlphaGoNode(parent=self, probability=prob)

If we have children, then we select one from them and play the move. We select using the following function in the AlphaGoNode:

def select_child(self):
  return max(
      self.children.items(), 
      key=lambda child: child[1].q_value + child[1].u_value
  )

After each simulation, we find the value of the value network and rollout by the fast policy, and then combine them using the equation:

$$ \text{weighted\_value} = (1 - \lambda) \cdot \text{value} + \lambda \cdot \text{rollout\_value} $$

After combining, we update the value of AlphaGoNode using the following function that we have in the node:

def update_values(self, leaf_value):
  if self.parent is not None:
      self.parent.update_values(leaf_value)

  self.visit_count += 1
  self.q_value += leaf_value / self.visit_count
  if self.parent is not None:
      c_u = 5
      self.u_value = (
          c_u
          * np.sqrt(self.parent.visit_count)
          * self.prior_value
          / (1 + self.visit_count)
      )

The rest is simple; we just take the child which is visited the most, and to save time, we avoid choosing positions like an eye. This is also partially because our agent doesn't have the ability to pass until it has no other option.

AlphaGo vs Agents

AlphaGo played as white in all matches, with no inherent advantage. It won every game except when AlphaGo faced itself, where black won. Something you need to note is that this version of AlphaGo only had 10 simulations, a depth of 30, and a rollout limit of 40 for the sake of computation. Even though by doing this, we are trading accuracy, it still manages to win an average of 60 games out of 100 against the supervised agent and the MCTS Agent with more rounds.

Extra Notes

AlphaGo uses an encoder which is much more complex than our simple encoder with 48 features, which I didn't implement because in our cases, since the board is small, our encoder works well. If you want to try that out, you can create a new encoder in the alphago/encoders.
This is already mentioned, but it's worth noting once more: we aren't training a different rollout model; instead, we're using the same model for self-play and rollout.
KGS pretty much has the entire or more data on which AlphaGo was trained.
If you want to use custom data, create a folder inside the dataset folder and pass the name to the dataloader.
The current version doesn't have the ability to pass a turn until and unless it doesn't have any legal move to choose. But the implementation is pretty much straightforward, as you will only have to tweak some small changes in the encoders and increase the output shape of networks other than policy by 1 for passing the turn.

References

David Silver et al. "Mastering the game of Go with deep neural networks and tree search." Nature, vol. 529, 2016, pp. 484-503. [Link].
Jeffrey Barratt et al. "Playing Go without Game Tree Search Using Convolutional Neural Networks." arXiv preprint arXiv:1907.04658, 2019. [PDF].
Kevin Ferguson and Max Pumperla. "Deep Learning and the Game of Go" [Link].
Richard S. Sutton and Andrew G. Barto. "Reinforcement Learning: An Introduction." MIT Press, 2018. [Link].