Google Summer of Code'23 - ML4SCI
Generated using Stability AI's DreamStudio
I'm thrilled to share that I've been selected for Google Summer of Code (GSoC) with my favorite organization Ml4SCI. I'll be working on developing equivariant neural networks for dark matter substructure with strong lensing.
I'll be mentored by:
Throughout the summer, I'll be documenting my work and sharing the things I learn. I hope you enjoy reading about my experiences and progress.
Project Abstract
Strong gravitational lensing is a promising probe of the substructure of dark matter to better understand its underlying nature. Deep learning methods have the potential to accurately identify images containing substructure and differentiate WIMP particle dark matter from other well-motivated models, including vortex substructure of dark matter condensates and superfluids. However, accurately identifying images containing substructure and differentiating between various dark matter models can be challenging. Deep learning methods, particularly equivariant neural networks, provide a promising approach to addressing these challenges. This project will focus on the further development of the DeepLense pipeline that combines state-of-the-art deep learning models with strong lensing simulations based on lenstronomy. The focus of this project is using equivariant neural networks for the classification and regression of dark matter particle candidates (e.g. CDM, WDM, axions, SIDM).
Gravitational Lensing
Gravitational lensing is a phenomenon where the gravity of massive objects, like clusters of galaxies or individual stars, distorts and magnifies the light of more distant objects behind them, allowing us to study the details of early galaxies too far away to be seen with current telescopes. Hubble observations have greatly increased the number of Einstein rings and helped create maps of dark matter in galaxy clusters. The lensed images of crosses, rings, arcs, and more not only provide intriguing visuals but also enable astronomers to probe the distribution of matter in galaxies and clusters of galaxies, as well as observe the distant universe. One promising method for studying the nature of dark matter is through strong gravitational lensing. By analyzing the perturbations in lensed images that cannot be explained by a smooth lens model, such as those caused by subhalos or line-of-sight halos, researchers can gain insights into the distribution and properties of dark matter.
Equivariant Neural Network
Equivariant neural networks are a type of neural network that can preserve the symmetries of input data, particularly data with group symmetries. They achieve this through the use of a group representation, which describes how a group acts on a vector space. The convolution operation, which is a key building block of many neural networks used in image and signal processing, is defined based on this group representation. Compared to standard convolutional neural networks, where filters are learned independently of the input data, in equivariant neural networks, the filters are learned as a function of the group representation. This ensures that the filters are consistent with the symmetries of the input data, making the learning process more efficient and allowing for better generalization. Different types of group representations, such as rotation, translation, or permutation representations, can be used in equivariant neural networks depending on the type of data being processed and the symmetry properties of the data.
Why Equivariant Neural Network?
E(2)-steerable Convolutional Neural Networks (CNNs) are neural networks that exhibit rotational and reflectional equivariance, meaning that their output remains independent of the orientation and reflection of the input image. This property can be demonstrated by feeding a randomly initialized E(2)-steerable CNN with rotated images, and visualizing the feature space of the network after a few layers. The feature space consisted of a scalar field and a vector field, which were color-coded and represented by arrows, respectively. The visualization showed that the feature space underwent equivariant transformations under rotations, and the output was stable under changes in the input image orientation. To further illustrate this stability, the feature space was transformed into a comoving reference frame by rotating the response fields back, resulting in a stabilized view of the output.
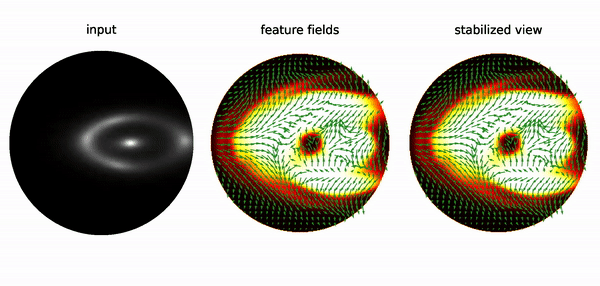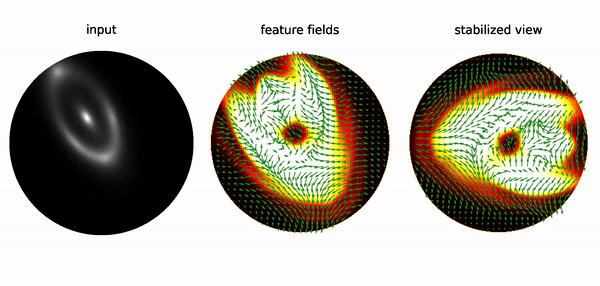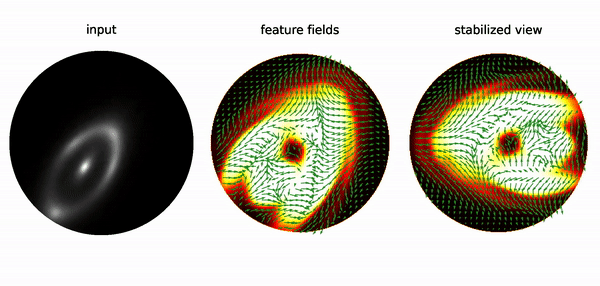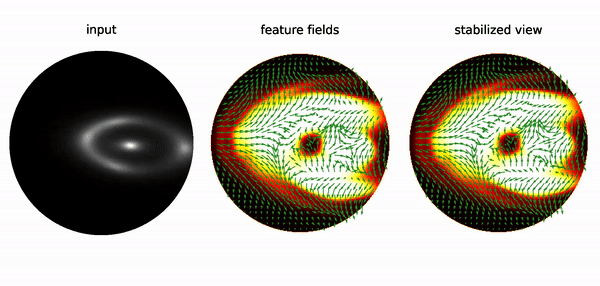
The invariance of the features in the comoving frame validates the rotational equivariance of E(2)-steerable CNNs empirically. Note that the fluctuations of responses are discretization artifacts due to the sampling of the image on a pixel grid, which does not allow for exact continuous rotations.
Conventional CNNs are not equivariant under rotations, leading to random variations in the response with changes in image orientation. This limits the ability of CNNs to generalize learned patterns between different reference frames. Equivariant neural networks, such as E(2)-steerable CNNs, address this limitation by ensuring that the feature space of the network undergoes a specified transformation behavior under input transformations. As a result, these networks effectively capture symmetries in the data, making them useful for tasks such as studying substructures in strong gravitational lensing images.
In summary, there are four major reasons to favor an equivariant neural network:
- Data Efficiency
- Equivariance in all layers
- Better generalizability
- Reduce Parameters
Why not Augmentation?
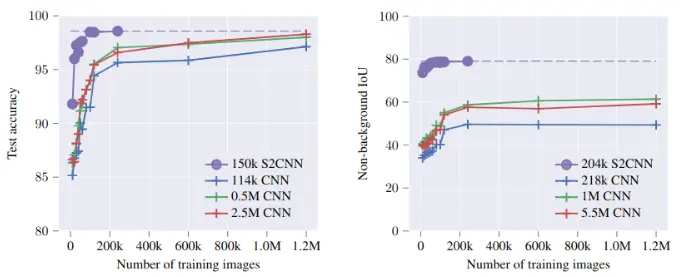
The answer to this question is explained in the paper "Equivariance versus Augmentation for Spherical Images" by Jan E Gerken et al. There, they analyze the role of rotational equivariance in convolutional neural networks applied to spherical images. They demonstrated that non-equivariant classification models require significant data augmentation to reach the performance of smaller equivariant networks. They also showed that the performance of non-equivariant semantic segmentation models saturates well below that of equivariant models as the amount of data augmentation is increased. Additionally, they found that the total training time for an equivariant model is shorter compared to a non-equivariant model with matched performance.
Models
E(2)-steerable CNN
Group equivariant Convolutional Neural Networks (G-CNNs), are a natural generalization of convolutional neural networks that reduces sample complexity by exploiting symmetries. The feature maps of a GCNN are functions over the elements of the group. A naive implementation of group convolution requires computing and storing a response for each group element. For this reason, the GCNN framework is not particularly convenient to implement networks equivariant to groups with infinite elements.
Steerable CNNs are a more general framework that solves this issue. The key idea is that, instead of storing the value of a feature map on each group element, the model stores the Fourier transform of this feature map, up to a finite number of frequencies.
Steerable CNNs are a neural network architecture that is equivariant to both 2D and 3D isometries, as well as equivariant MLPs. Equivariant neural networks ensure that the transformation behavior of their feature spaces is specified under transformations of their input. For example, conventional CNNs are designed to be equivariant to translations of their input, meaning that a translation of image results in a corresponding translation of the network's feature maps. However, E(n)-equivariant models, including steerable CNNs, are guaranteed to generalize over a broader range of transformations which includes translation, rotation, and reflection, and are thus more data-efficient than conventional CNNs.
The feature spaces of E(n)-equivariant steerable CNNs are defined as spaces of feature fields characterized by their transformation law under rotations and reflections. Examples of such feature fields include scalar fields (such as grayscale images or temperature fields) and vector fields (such as optical flow or electromagnetic fields).
Equivariant Transformer Networks
Equivariant Transformer (ET) layers are image-to-image mappings that incorporate prior knowledge on invariances with respect to continuous transformation groups. ET layers can be used to normalize the appearance of images before classification (or other operations) by a convolutional neural network.
Harmonic Net
Harmonic Networks or H-Nets are a type of convolutional neural network (CNN) that exhibits equivariance to patch-wise translation and 360-rotation, which is not the case for regular CNNs, where global rotation equivariance is typically sought through data augmentation. They achieve this by using circular harmonics instead of regular CNN filters, which return a maximal response and orientation for every receptive field patch. H-Nets use a rich, parameter-efficient, and low computational complexity representation, and deep feature maps within the network encode complicated rotational invariants.
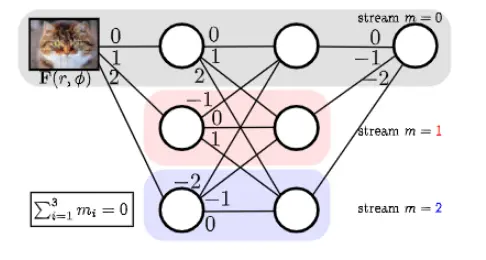
There are a few advantages to using Harmonic nets:
- Good generalization for insufficient data
- Few parameters
- Interpretable features for rotation
- No rotational data augmentation
Equivariant Wide ResNet
The e2wrn (Equivariant Wide ResNet) is a technique to attain equivariance in ResNet. It utilizes the codebase available at Wide ResNet as its foundation and can be constructed using escnn/e2cnn.
Publications
Geo Jolly Cheeramvelil*, Sergei V Gleyzer, Michael W Toomey, "Equivariant Neural Network for Signatures of Dark Matter Morphology in Strong Lensing Data", Machine Learning for Physical Sciences 2023