The term dynamic programming (DP) refers to a collection of algorithms that can be used to compute optimal policies given a perfect model of the environment as a Markov decision process. Classical DP algorithms are not used much due to its assumption of a perfect model, and great computational expenses.

In DP, we usually assume that the environment is a finite MDP. That is, we assume that state, action, and reward sets, $\mathcal{S}, \mathcal{A}, \mathcal{R}$, are finite, and that its dynamics are given by a set of probabilities $p(s’,r|s,a)$, for all $s\in \mathcal{S}, a\in \mathcal{A}, r\in \mathcal{R}$, and $s’\in \mathcal{S}^+$. Although DP ideas can be applied to continuous states, exact solutions are possible only in special cases. In order to obtain approximate solutions for tasks with continuous states and actions, we quantize the state and action spaces and then apply finite-state DP.

The key idea of DP is the use of value functions to organize and search for good policies. We can easily obtain optimal policies once we have found the optimal value functions, $v_\star$ or $q_\star$, which satisfy the Bellman optimality equations:
\(\begin{align} v_\star(s) &= \max_a \mathbb{E}[R_{t+1} + \gamma v_\star(S_{t+1}) | S_t = s, A_t = a] \\ &= \max_a \sum_{s', r} p(s',r|s,a)\left[r + \gamma v_\star(s')\right] \\ \end{align}\)

or,
\(\begin{align} q_\star(s,a) &= \mathbb{E}[R_{t+1} + \gamma \max_{a'} q_\star(S_{t+1}, a') | S_t = s, A_t = a] \\ &= \sum_{s', r} p(s',r|s,a)\left[r + \gamma \max_{a'} q_\star(s',a')\right] \\ \end{align}\)

for all $s\in \mathcal{S}, a\in \mathcal{A}$, and $s’\in \mathcal{S}^+$.

Policy Evaluation

Policy evaluation is the process of computing the state-value function $v_\pi$ for an arbitrary policy $\pi$. It is also referred to as the prediction problem.

We know that:

\[\begin{align} v_\pi(s) &\: \dot{=} \: \mathbb{E}_\pi[R_{t+1} + \gamma G_{t+1} | S_t = s] \\ &= \mathbb{E}_\pi[R_{t+1} + \gamma v_\pi(S_{t+1}) | S_t = s] \\ &= \sum_a \pi(a|s) \sum_{s', r} p(s',r|s,a)\left[r + \gamma v_\pi(s')\right] \label{eq1}\tag{1} \end{align}\]

where, $\pi(a|s)$ is the probability of taking action $a$ in state $s$ under the policy $\pi$. The existence and uniqueness of $v_\pi$ are guaranteed as long as either $\gamma < 1$ or eventual termination is guaranteed from all states under the policy $\pi$.

If the environment’s dynamics are completely known, then \ref{eq1} is a system of $|\mathcal{S}|$ simultaneous linear equations in $|\mathcal{S}|$ unknowns. Here, iterative methods are most suitable for solving this system. Consider a sequence of approximate value functions $v_0, v_1, v_2 \dots, $ each mapping $\mathcal{S}^+$ to $\mathbb{R}$. The initial approximation, $v_0$, is chosen arbitrarily(except terminal state, which is zero), and each successive approximation is obtained by using the Bellman equation for $v_\pi$ as an update rule:

\[\begin{align} v_{k+1} &\: \dot{=} \: \mathbb{E}_\pi[R_{t+1} + \gamma v_k(S_{t+1}) | S_t = s] \\ &= \sum_a \pi(a|s) \sum_{s', r} p(s',r|s,a)\left[r + \gamma v_k(s')\right] \\ \end{align}\]

for all $s\in \mathcal{S}$. Clearly, $v_k = v_\pi$ is a fixed point for this update rule because the Bellman equation for $v_\pi$ assures us of equality in this case. Indeed, the sequence ${v_k}$ will converges to $v_\pi$ as $k \rightarrow \infty$. This algorithm is called iterative policy evaluation.

To produce each successive approximation, $v_{k+1}$ from $v_k$, iterative policy evaluation applies the same operation to each state $s$: it replaces the old value of $s$ with new value obtained from the old values of the successor states of $s$, and the expected immediate rewards, along all the one-step transitions possible under the policy being evaluated. This kind of operations are called as expected update Each iteration of iterative policy evaluation updates the value of every state all at once to produce the next approximate value function, $v_{k+1}$.

Pseudo-Code

Formally, an iterative policy only converges at its limit, but in practice it must be halted. The pseudocode tests the quantity $\max_{s \in \mathcal{S}} | v_{k+1} - v_k |$ after each iteration, and halts when it is less than a threshold.

Iterative Policy Evaluation, for estimating $V \approx v_\pi$
  1. Input $\pi$, the policy to be evaluated.
  2. Algorithm parameter: a small threshold $\theta > 0$ determining accuracy of estimation.
  3. Initialize $V(s)$, for all $s \in \mathcal{S}$, arbitrarily except that $V(\text{terminal}) = 0$.
  4. Loop:
    • $\Delta \leftarrow 0$
    • Loop for each $s \in \mathcal{S}$:
      • $v \leftarrow V(s)$
      • $V(s) \leftarrow \sum_a \pi(a|s) \sum_{s', r} p(s',r|s,a)\left[r + \gamma V(s')\right]$
      • $\Delta \leftarrow \max(\Delta, | V(s) - v |)$
  5. Until $\Delta < \theta$

Policy Improvement

Suppose we determined the value function $v_\pi$ for an arbitrary deterministic policy $\pi$, and we want to know whether it is good to choose an action $a \neq \pi(s)$ by changing the policy or not. One way to perform this is to choose an action in $s$ and thereafter following the policy, $\pi(s)$. The value will be $q_\pi(s, a)$. The main thing is whether this is greater than or less than the $v_\pi(s)$. If it is greater, that is if it is better to choose $a$ once in $s$ and then follow the $\pi$ again, then we can say that is better than to follow $\pi$ always- then one would expect it to be better still to select $a$ every time $s$ is encountered, and that the new policy would in fact be better one overall. This is a special case of a general result called the policy improvement theorem.

Let $\pi$ and $\pi’$ be any pair of deterministic policies such that, for all $s \in \mathcal{S}$,

\[q_\pi(s, \pi'(s)) \geq v_\pi(s)\]

Then the policy $\pi’$ must be as good as, or better than, $\pi$. That is, it must obtain greater or equal expected returns from all states $s \in \mathcal{S}$:

\[v_{\pi'}(s) \geq v_\pi(s)\]

Morever if $q_\pi(s, \pi’(s)) > v_\pi(s)$ then $\pi’$ is definitely better than $\pi$. This result applies in particular to the two policies, an original deterministic policy, $\pi$, and a changed policy, $\pi’$, that is identical to $\pi$ expect that $\pi’(s) = a \neq \pi(s)$. This result holds at all states other than $s$. Thus if $q_\pi(s, a) > v_\pi(s)$, then the changed policy is indeed better than $\pi$. Proof for the same is given below:

\[\begin{align} v_\pi(s) &\leq q_\pi(s, \pi'(s)) \\ &= \mathbb{E}[R_{t+1} + \gamma v_\pi(S_{t+1}) | S_t = s, A_t = \pi'(s)] \\ &= \mathbb{E}_{\pi'}[R_{t+1} + \gamma v_\pi(S_{t+1}) | S_t = s] \\ &\leq \mathbb{E}_{\pi'}[R_{t+1} + \gamma q_\pi(S_{t+1}, \pi'(S_{t+1})) | S_t = s] \\ &= \mathbb{E}_{\pi'}[R_{t+1} + \gamma \mathbb{E}_{pi'}[R_{t+2} + \gamma v_\pi(S_{t+2}) | S_{t+1}, A_{t+1} = \pi'(S_{t+1})] | S_t = s] \\ &= \mathbb{E}_{\pi'}[R_{t+1} + \gamma R_{t+2} + \gamma^2 v_\pi(S_{t+2}) | S_t = s] \\ &\leq \mathbb{E}_{\pi'}[R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \gamma ^3 v_\pi(S_{t+3}) | S_t = s] \\ &\vdots \\ &\leq \mathbb{E}_{\pi'}[R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \cdots + | S_t = s] \\ &= v_{\pi'}(s) \end{align}\]

It is natural to choose the best action according to $q_\pi(s, a)$. In other words, to consider the new greedy policy, $\pi’$, given by

\[\begin{align} \pi'(s) &= \arg\max_a q_\pi(s, a) \\ &= \arg\max_a \mathbb{E}[R_{t+1} + \gamma v_\pi(S_{t+1}) | S_t = s, A_t = a] \\ &= \arg\max_a \sum_{s', r} p(s',r|s,a)\left[r + \gamma v_\pi(s')\right] \\ \end{align}\]

The greedy policy takes the action that looks best in short term - after one step of lookahead - according to $v_\pi$. The greedy policy meets the conditions of policy improvement theorem, so that it is good as, or better than, $\pi$. The process of making a new policy that improves on an original policy, by making it greedy with respect to the value function of original policy, is called policy improvement. Policy improvement must be able to give strictly better policies than the original policy except when the original policy is already optimal.

Policy Iteration

Once a policy, $\pi$, has been improved using $v_\pi$ to yield a better policy $\pi’$, we can compute $v_{\pi’}$ and improve it again to yield an even better policy $\pi’’$. We can thus obtain a sequence of monotonically improving policies and value functions:

\[\begin{align} \pi_0 \overset{E}{\rightarrow} v_{\pi_0} \overset{I}{\rightarrow} \pi_{1} \overset{E}{\rightarrow} v_{\pi_{1}} \overset{I}{\rightarrow} \pi_2 \cdots \overset{I}{\rightarrow} \pi_{*} \overset{E}{\rightarrow} v_{\pi_{*}} \end{align}\]

where $\overset{E}{\rightarrow}$ denotes a policy evaluation, and $\overset{I}{\rightarrow}$ denotes a policy improvement. Each policy is guaranteed to be strict improvement over the previous one unless the previous policy is optimal. Because a finite MDP has only a finite number of policies, the process must converges to an optimal policy and optimal value funtion in a finite number of steps.

This way of finding an optimal policy is called policy iteration.

Pseudo-Code

Policy Iteration (using iterative policy evaluation) for estimating $\pi \approx \pi_*$.
  • 1. Initialization
    1. $V(s) \in \mathbb{R}$ and $\pi(s) \in \mathcal{A}(s)$ arbitrarily $\forall s \in \mathcal{S}$
  • 2. Policy Evaluation
    1. Loop:
      • $\Delta \leftarrow 0$
      • Loop for each $s \in \mathcal{S}$:
        • $v \leftarrow V(s)$
        • $V(s) \leftarrow \sum_{s', r} p(s',r|s,a)\left[r + \gamma V(s')\right]$
        • $\Delta \leftarrow \max(\Delta, | V(s) - v |)$
    2. Until $\Delta < \theta$ (a small positive number determining the accuracy of estimation)
  • 3. Policy Improvement
    1. policy-stable $\leftarrow$ true
    2. For each $s \in \mathcal{S}$:
      1. old-action $\leftarrow$ $\pi(s)$
      2. $\pi(s) \leftarrow \arg\max_a \sum_{s', r} p(s',r|s,a)\left[r + \gamma V(s')\right]$
      3. If old-action $\neq$ $\pi(s)$, then policy-stable $\leftarrow$ false
    3. If policy-stable, then stop and return $V \approx v_\star$ and $\pi \approx \pi_*$; else go to 2

    • Value Iteration

    In policy iteration, we can see policy evaluation taking prolonged iterative computations which requires multiple sweeps through the state set. The policy evaluation which is done iteratively, converge exactly to $v_\pi$ only in its limit. So instead of this, we have several ways to truncate it without losing the convergence guarantees of the policy iteration. One important special case is when policy evaluation is stopped after one sweep through the state set. This is called value iteration. It can be written as a simple update operation:

    \[\begin{align} v_{k+1}&\:\dot{=}\:\max_a \mathbb{E}[R_{t+1} + \gamma v_k(S_{t+1}) | S_t = s, A_t = a] \\ &= \max_a \sum_{s', r} p(s',r|s,a)\left[r + \gamma v_k(s')\right] \\ \end{align}\]

    For arbitrary $v_0$, the sequence ${v_k}$ can be shown to converge to $v_\star$, under the same conditions that guarantee the existence of $v_\star$.

    Pseudo-Code

    Value Iteration, for estimating $\pi \approx \pi_*$.
  • Algorithm parameter: a small threshold $\theta > 0$ determining accuracy of estimation
  • Initialize $V(s)$, for all $s \in \mathcal{S}^+$, arbitrarily except $V(\text{terminal}) = 0$
  • Loop:
    • $\Delta \leftarrow 0$
    • Loop for each $s \in \mathcal{S}:$
      • $v \leftarrow V(s)$
      • $V(s) \leftarrow \max_a \sum_{s', r} p(s',r|s,a)\left[r + \gamma V(s')\right]$
      • $\Delta \leftarrow \max(\Delta, | V(s) - v |)$
  • Until $\Delta < \theta$
  • Output a deterministic policy $\pi \approx \pi_*$, such that $\pi(s) = \arg\max_a \sum_{s', r} p(s',r|s,a)\left[r + \gamma V(s')\right]$

    • Asynchronous Dynamic Programming

    Major drawback of dynamic programming is that it involves operations over entire state set of the MDP. This is a problem for large MDPs. In this case, even a single sweep would be too costly. Asynchronous Dynamic Programming algorithms are in-place DP algorithms that are not organized in terms of systematic sweeps of the state set. These algorithms update values of states in any order, using whatever values of other states are available. Values of some states may be updated several times before others. To converge correctly, this algorithm must continue to update values of all the states: it cannot ignore any states after some point in the computation. Avoiding sweeps does not necessarily mean less computation. It just avoid long sweeps before it can make progress improving a policy. We can try to order the updates to let value information propagate from state to state in an efficient manner. Sometimes it is also possible to skip updating some states entirely if they are not relavant to the optimal behavior. Asynchronous algorithms also make it easier to intermix computation with real-time interaction. To solve a given MDP, we can run DP algorithm at the same time that an agent is actually experiencing the MDP. The agent’s experience can be used to determine the states to which the DP algorithm should update. At the same time, latest policy and value information can guide the agent’s decision making.

    Generalized Policy Iteration

    Policy iteration consist of two steps:(1) policy evaluation, which makes the value function consistent with the current policy, and (2) policy improvement, which makes the policy greedy with respect to the current value function. In policy iteration, these two processes alternate, each completing before the next begins, but isn’t necessary. In value iteration, for example, only a single iteration of policy evaluation is performed in between each policy improvement. In asynchronous DP, the evaluations and improvement processes are interleaved. In some case a single state is updated in one process before returning to the other. As long as both process continue to update all the states, the algorithm will lead to the convergance of an optimal value function and an optimal policy.

    The term Generalized Policy Iteration (GPI) refers to the general idea of letting policy-evaluation and policy-improvement process interact, independent of the granularity and other details of the process. Almost all RL methods are well described as GPI. That is, all have identifiable policy and value functions, with policy always being improved with respect to the value function and the value function always being driven towards the value function for the policy. If both the evaluation and improvement process stabilize, the the value function and the policy are optimal.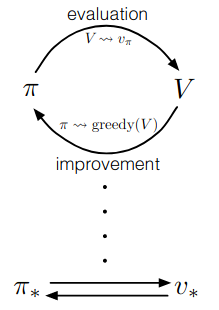

    The evaluation and improvement processes in GPI can be viewed as both competing and cooperating. The policy is greedy with respect to the value function which makes value function incorrect for the changed policy, and making the value function consistent with the policy makes that policy no longer to be greedy. In the long run, the value function will converge to the optimal value function and the policy will converge to the optimal policy.

    Efficiency of Dynamic Programming

    DP algorithms are not practical for very large problems, but is efficient compared to other methods. A DP methods is guaranteed to find an optimal policy in polynomial time even through the total number of policies is $k^n$, where $n$ denotes number of states and $k$ denotes the number of actions. DP is sometimes thought to be of limited applicability because of curse of dimensionality, the fact that the number of states often grows exponentially with the number of state variables. On problems with large state space, asynchronous DP methods are often preferred. Asynchronous methods and other variations of GPI can be applied in such cases and may find good or optimal policies much faster than synchronous methods can.

    Problems

    1. In Example 4.1, if⇡ $\pi$ is the equiprobable random policy, what is $q_\pi(11,\text{down})$? What is $q_\pi(7,down)$?

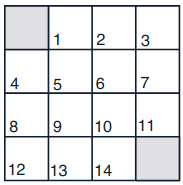
      $q_\pi(11,\text{down})$ = -1 + 1*$q_\pi(T, \text{exit})$ = -1

      $q_\pi(7,down)$ = -1 + 1*$v_\pi(11)$ = -15

    2. In Example 4.1, suppose a new state 15 is added to the gridworld just below state 13, and its actions, left, up, right, and down, take the agent to states 12, 13, 14,and 15, respectively. Assume that the transitions from the original states are unchanged. What, then, is $v_\pi(15)$ for the equiprobable random policy? Now suppose the dynamics of state 13 are also changed, such that action down from state 13 takes the agent to the new state 15. What is $v_\pi(15)$ for the equiprobable random policy in this case?

      1. $v_\pi(s) = \sum_a \pi(a|s) \sum_{s’, r} p(s’,r|s,a)\left[r + \gamma v_\pi(s’)\right]$
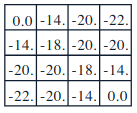
        \(\begin{align} v_\pi(15) &= \frac{1}{4}[-1 + v_\pi(12) + -1 + v_\pi(13) + -1 + v_\pi(15)] \\ &= \frac{1}{4}[-4 + -22 + -20 + -14 + v_\pi(15)] \\ \end{align}\)
        \(\begin{align} 4\times v_\pi(15) &= -60 + v_\pi(15) \\ v_\pi(15) &= \frac{-60}{3} \\ &= -20 \end{align}\)

      2. Before state 15 came, $v_\pi(13)$ was $-20$. After state 15 came,
        \(\begin{align} v_\pi(13) &= \frac{1}{4}[-1 + -22 + -1 + -20 + -1 + -14 + -1 + v_\pi(15)] \\ &= \frac{1}{4}[-60 + v_\pi(15)] \\ & = -15 + 0.25\times v_\pi(15) \\ v_\pi(15) &= \frac{1}{4}[-1 + -22 + -1 + v_\pi(13) + -1 + -14 + -1 + v_\pi(15)] \\ &= \frac{1}{4}[-40 + v_\pi(15) + v_\pi(13)] \\ &= \frac{1}{4}[-40 + v_\pi(15) + -15 + 0.25\times v_\pi(15)] \\ &= \frac{1}{4}[-55 + 1.25 \times v_\pi(15)] \\ 4\times v_\pi(15) &= -55 + 1.25 \times v_\pi(15) \\ v_\pi(15) &= \frac{-55}{2.75} = -20\\ \end{align}\)

    3. What are the equations analogous to (4.3), (4.4), and (4.5) for the action-value function $q_\pi$ and its successive approximation by a sequence of functions $q_0, q_1, q_2, \dots$

      4.3. $q_\pi(s, a) = \mathbb{E}_\pi[R_{t+1} +\gamma \sum_{a’} \pi(a’|S_{t+1})q_\pi(S_{t+1}, a’) | S_t = s, A_t = a]$

      4.4. $q_\pi(s, a) = \sum_{s’, r} p(s’,r|s,a)\left[r + \gamma \sum_{a’} \pi(a’|s’)q_\pi(s’, a’)\right]$

      4.4. $q_{k+1}(s) = \sum_{s’, r} p(s’,r|s,a)\left[r + \gamma \sum_{a’} \pi(a’|s’)q_{k}(s’, a’)\right]$

    4. The policy iteration algorithm on page 80 has a subtle bug in that it may never terminate if the policy continually switches between two or more policies that are equally good. This is ok for pedagogy, but not for actual use. Modify the pseudocode so that convergence is guaranteed.

      In policy improvement we should not only consider the $\pi(s)$ to establish the stability of the policy, but also the value function $v_\pi(s)$. If change of $v_\pi(s)$ is more than zero, then the policy isn’t stable.

    5. How would policy iteration be defined for action values? Give a complete algorithm for computing $q_\star$, analogous to that on page 80 for computing $v_\star$. Please pay special attention to this exercise, because the ideas involved will be used throughout the rest of the book.

      1. 1. Initialization
        1. $Q(s, a) \in \mathbb{R}$ and $\pi(s) \in \mathcal{A}(s)$ arbitrarily $\forall s \in \mathcal{S}$
      2. 2. Policy Evaluation
        1. Loop:
          • $\Delta \leftarrow 0$
          • Loop for each $s \in \mathcal{S}$:
            • $q \leftarrow Q(s, a)$
            • $Q(s) \leftarrow \sum_{s', r} p(s',r|s,a)\left[r + \gamma \sum_{a'} \pi(a'|s')q_\pi(s',a')\right]$
            • $\Delta \leftarrow \max(\Delta, | Q(s,a) - q |)$
        2. Until $\Delta < \theta$ (a small positive number determining the accuracy of estimation)
      3. 3. Policy Improvement
        1. policy-stable $\leftarrow$ true
        2. For each $s \in \mathcal{S}$:
          1. old-action $\leftarrow$ $\pi(s)$
          2. $\pi(s) \leftarrow \sum_{s', r} p(s',r|s,a)\left[r + \gamma \sum_{a'} \pi(a'|s')q_\pi(s',a')\right]$
          3. If old-action $\neq$ $\pi(s)$, then policy-stable $\leftarrow$ false
        3. If policy-stable, then stop and return $Q \approx q_\star$ and $\pi \approx \pi_*$; else go to 2

    6. Suppose you are restricted to considering only policies that are $\epsilon$-soft, meaning that the probability of selecting each action in each state, $s$, is at least $\epsilon/|A(s)|$. Describe qualitatively the changes that would be required in each of the steps 3, 2, and 1, in that order, of the policy iteration algorithm for $v_\star$ on page 80.

      1. Step 1 - No change
      2. Step 2 - No change

      3. Step 3 - We should change the improved policy

        \[\begin{align} \pi(s) &= \begin{cases} 1 - \epsilon, \quad\text{ if } a = \arg\max_a \sum_{s',r} p(s',r|s,a) \left[r + \gamma V(s',a)\right] \\ \epsilon/\|A(s)\|, \quad\text{ otherwise} \end{cases} \end{align}\]

    7. Write a program for policy iteration and re-solve Jack’s car rental problem with the following changes. One of Jack’s employees at the first location rides a bus home each night and lives near the second location. She is happy to shuttle one car to the second location for free. Each additional car still costs $ 2$, as do all carsmoved in the other direction. In addition, Jack has limited parking space at each location.If more than 10 cars are kept overnight at a location (after any moving of cars), then an additional cost of $4 must be incurred to use a second parking lot (independent of how many cars are kept there). These sorts of non linearities and arbitrary dynamics often occur in real problems and cannot easily be handled by optimization methods other than dynamic programming. To check your program, first replicate the results given for the original problem.

      Code

    8. Why does the optimal policy for the gambler’s problem have such a curious form? In particular, for capital of 50 it bets it all on one flip, but for capital of 51 it does not. Why is this a good policy?

      We can see that $p_h$ is less than 0.5 and $\gamma = 1$ for this case. That means the agent tries to maximize the reward at each step, but doesnt care much about the time steps. Since $p_h < 1$, we have more chance to lose. In this case its actually better to bet safely such that even if we lose we get an another chance to win. For the particular case of 50, if we win then it reachs goal in one step. But for 51, we can first bet with 1 dollar, if we lose then we can bet all 50 dollars, which might be a better option. Similarly, for 70, its better to bet 20 otherwise if we use 30 and lose, we only have 40 dollars to bet, which denies the possiblity to win in one step(40+40 never is 100).

    9. Implement value iteration for the gambler’s problem and solve it for $p_h=0.25$ and $p_h=0.55$. In programming, you may find it convenient to introduce two dummy states corresponding to termination with capital of 0 and 100, giving them values of 0 and 1 respectively. Show your results graphically, as in Figure 4.3. Are your results stable as $\theta \rightarrow 0$?

      Yes, Code