Finite Markov Decision Processes
- The Agent-Environment Interface
- Goals and Rewards
- Returns and Episodes
- Unified Notation for Episodic and Continuing Tasks
- Policies and Value Functions
- Optimal Policies and Optimal Value Functions
- Problems
Finite Markov Decision Processes, or finite MDPs are problems which involves evaluative feedback, but also an associative aspect - choosing different actions based on the situations. MDPs are a classic formalization of sequential decision making, where actions influences not just the immediate reward, but the subsequent situations,or states, and through those future rewards. Thus MDPs involves delayed reward and the need to tradeoff immediate and delayed rewards. In MDP we estimate $q^\star(s, a)$ in each states $s$ for action $a$,or we estimate the value $v^\star(s)$ for each state given optimal action selections, where we only estimate $q^\star(a)$ in the bandit problem. These state-dependent quantities are essential to accurately assigning credit for long-term consequences to individual action selections.
The Agent-Environment Interface
The learner and decision maker is called an agent. The things which agent interact, comprising everything outside the agent is called the environment. The agent chooses an action and the environment responds to these actions and present new situations to the agent continuously. The environment also give rise to rewards; the values that agent seeks to maximize over the time.
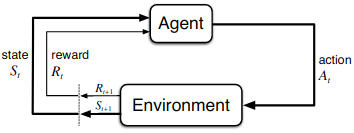
In other words, the agent and environment interacts with each other during a sequence of time steps, $t = 0, 1, 2, \dots$. At each time step $t$, the agent receive some representation of the environment’s state, $S_t \in \mathcal{S}$, and on that the agent select an action, $A_t \in \mathcal{A}(s)$. One time step later, the agent receives a numerical reward, $R_{t+1} \in \mathcal{R} \subset \mathbb{R}$, and enters a new state $S_{t+1}$. In finite MDP, the sets of states, actions and rewards all have a finite number of elements. In this case, the random variables $R_t$ and $S_t$ have well defined discrete probability distribution which depends on the preceding state and action. i.e. there is a probability that $s’ \in \mathcal{S}$ and $r \in \mathcal{R}$ occurs at time $t$, given the values of preceding state and action:
\[\begin{align} p'(s', r | s, r) \dot{=} Pr\{S_t = s', R_t =r | S_{t-1} = s, A_{t-1} = a\} \end{align}\]for all $s’,s \in \mathcal{S}, r \in \mathcal{R} ,$ and $a \in \mathcal{A}(s)$. The dot over equal sign means that it is definition rather than a fact. The dynamic function: $p: \mathcal{S} \times \mathcal{R} \times \mathcal{S} \times \mathcal{A} \rightarrow [0, 1]$ is an ordinary deterministic function of four arguments. $p$ specifies a probability distribution for each choice of $s$ and $a$, that is:
\[\begin{align} \underset{s' \in \mathcal{S}}{\sum} \underset{r \in \mathcal{R}}{\sum} p(s', r | s, a) = 1, \forall s \in \mathcal{S}, a \in \mathcal{A}(s) \end{align}\]In a markov decision process, the probabilities given by $p$ completely characterize the environment’s dynamics. That is, the probability of each possible value of $S_t$ and $R_t$ depends only on the immediately preceding state and action, but not on the earlier states. This actually is a restriction on the state, but not decision process. The state must include information about all aspects of the past agent-environment interaction that make a difference for the future. Then the state is said to have the Markov Property.
From the four-argument dynamics function $p$, we can anything about the environment like:
-
state-transition probabilities
\(\begin{align} p(s' | s, a) \: &\dot{=}\: Pr\{S_t = s' | S_{t-1} = s, A_{t-1} = a\} \\ \: &\dot{=}\: \underset{r \in \mathcal{R}}{\sum} p(s', r | s, a) \\ \end{align}\) -
expected rewards for state-action pairs
\(\begin{align} r(s,a) \: &\dot{=}\: \mathbb{E}[R_t | S_{t-1} = s, A_{t-1} = a] \\ \: &\dot{=}\: \underset{r \in \mathcal{R}}{\sum} r \underset{s' \in \mathcal{S}}{\sum} p(s', r | s, a) \\ \end{align}\) -
expected rewards for state-action-next-state triples
\(\begin{align} r(s,a,s') \: &\dot{=}\: \mathbb{E}[R_t | S_{t-1} = s, A_{t-1} = a, S_{t} = s'] \\ \: &\dot{=}\: \underset{r \in \mathcal{R}}{\sum} r \frac{p(s', r | s, a)}{p(s' | s, a)} \\ \end{align}\)
Goals and Rewards
In Reinforcement Learning, the purpose or goal of an agent is formalized in terms of a special signal, called reward, passing from environment to the agent. At each time step, the reward is a simple number, $R_t \in \mathbb{R}$, and the agent is expected to maximize the rewards, but instead of maximizing the immediate reward, it should be able to maximize the cumulative reward in the long term. In short, that all of what we mean by goals and purposes can be well thought of as the maximization of the expected value of the cumulative sum of a received scalar signal (called reward).
It is critical that the rewards we set up truly indicates what we want to accomplish. In other words, it should be clear what the agent is trying to achieve, but not how it is trying to achieve it. The reward signal is not for imparting prior knowledge about how to achieve. For example, in chess if we reward agent for taking opponent’s piece, it might end up that agent will try to take pieces instead of winning. Therefore, the reward signal should represent what to achieve, but not how to achieve it.
Returns and Episodes
The agent’s goal is to maximize the cumulative rewards it receives in a long term.
In general, we try to maximize the expected return, where the return, denoted $G_t$, is defined as some specific function of the reward sequence. In simplest case it is the sum of rewards:
$G_t \: \dot{=}\: R_{t+1} + R_{t+2} + \dots + R_{t+T}$,
where $T$ is a final time step. This approach makes sense in applications with a final step, that is, when the agent-environment interaction breaks naturally into subsequences, which is called as episodes. Each episode ends in a special state called the terminal state, followed by a reset to a standard starting state or to s sample from a standard distribution of starting states. The next episode is independent of the previous episode. Thus episodes can be considered to end in the same terminal state, but with different rewards for different outcomes. Tasks with episodes are called episodic tasks. In episoidic tasks, we denote all nonterminal states as $\delta$ and set of all states with the terminal state, as $\delta^+$. The time of termination, $T$, is a random variable that normally varies from episode to episodes.
But in many cases the agent-environment interaction doesn’t break naturally into identifiable episodes, but goes on continuously without any limit. We call these continuing tasks. The above mentioned return formula is not applicable in this case because final time step would be $T = \infty$, and the return, which we are trying to maximize might also be infinite.
The concept which we use to solve this is discounting. According to this approach, the agent tries to select actions so that sum of discounted rewards it receives over the future is maximized. In particular, it chooses $A_t$ to maximize the expected discounted return, which is defined as:
$G_t \: \dot{=} \: R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \dots = \sum_{i=0}^{\infty} \gamma^{i} R_{t+i+1}$,
where $\gamma$ is discount rate, and $0 \leq \gamma \leq 1$.
The discount rate determines the present value of future rewards: a reward received $k$ time steps in future is only worth $\gamma^{k-1}$ times that of the immediate reward. If $\gamma < 1$, the infinte sum of discounted rewards has a finite value aslong as the reward sequence ${R_k}$ is bounded. If $\gamma = 0$, the agent is concerned about maximizing only the immediate rewards. But acting to maximize the immediate reward can reduce access to future reward and thus return is reduced. As $\gamma$ approaches 1, the return objective takes future rewards more strongly.
Returns at successive time steps are related to each other in a way:
\[\begin{align} G_t \: &\dot{=} \: R_{t+1} + \gamma G_{t+2} + \gamma^2 G_{t+3} + \dots \\ &\dot{=} \: R_{t+1} + \gamma \left( R_{t+2} + \gamma G_{t+3} + \dots \right) \\ &\dot{=} \: R_{t+1} + \gamma G_{t+1} \end{align}\]Unified Notation for Episodic and Continuing Tasks
We can rewrite the return formula as:
\[G_t \: \dot{=} \: \sum_{k=t+1}^T \gamma^{k-t-1} R_{k}\]including the possiblity that $T = \infty$ or $\gamma = 1$.
Policies and Value Functions
Almost all reinforcement learning algorithms involves estimating value functions- functions of state, or state-action pair that estimates how good it is for an agent to be in a given state. Value functions are defined with respect to particular ways of acting, aclled policies.
Formally, a policy is a mapping from states to probabilities of selecting each possible action. If the agent follows policy $\pi$ at time $t$, then $\pi(a|s)$ is the probability that $A_t = a$ if $S_t = s$. Reinforcement learning methods specify how the agent’s policy is changed as a result of it’s experience.
The value function of a state $s$ under a policy $\pi$, denoted $v_\pi(s)$, is the expected return when starting in $s$ and following a policy $\pi$. For MDPs, the value function is defined as:
\[\begin{align} v_\pi(s) &\: \dot{=} \: \mathbb{E}_{\pi}[G_t | S_t = s] \\ &= \mathbb{E}_{\pi}\left[\sum_{k=0}^{\infty} \gamma^{k} R_{k} \middle| S_t = s\right] \\ \end{align}\]where $\mathbb{E}_{\pi}$ is the expected value of a random variable given that agent follows policy $\pi$. The value of a terminal state is zero. We call the function $\pi$ the state-value function for policy $\pi$.
Similarly, the value of taking action $a$ in a state $s$ under a policy $\pi$, denoted $q_\pi(s,a)$, is the expected return when starting in $s$ and taking action $a$ under a policy $\pi$. It is defined as:
\[\begin{align} q_\pi(s, a) &\: \dot{=} \: \mathbb{E}_{\pi}[G_t | S_t = s, A_t = a] \\ &= \mathbb{E}_{\pi}\left[\sum_{k=0}^{\infty} \gamma^{k} R_{k} \middle| S_t = s, A_t = a\right] \\ \end{align}\]We call $q_\pi$ the action-value function for policy $\pi$.
A fundamental property of value functions is that they satisfy recursive relationships. For any policy $\pi$ and any state $s$, the following consistency condition holds between the value of $s$ and the value of its possible successor states:
\[\begin{align} v_\pi(s) &= \mathbb{E}_{\pi}[G_t | S_t = s] \\ &= \mathbb{E}_{\pi}[R_{t+1} + \gamma G_{t+1} | S_t = s] \\ &= \sum_a \pi(a|s) \mathbb{E}_{\pi}[R_{t+1} + \gamma G_{t+1} | S_t = s, A_t = a] \\ &= \sum_a \pi(a|s) \left[\mathbb{E}_{\pi}[R_{t+1} | S_t = s, A_t = a] + \mathbb{E}_{\pi}[\gamma G_{t+1} | S_t = s, A_t = a]\right] \\ \end{align}\]Diving the equations in brackets into part:
- $\mathbb{E}_{\pi}[R_{t+1} | S_t = s, A_t = a]$
- $\mathbb{E}_{\pi}[\gamma G_{t+1} | S_t = s, A_t = a]$
Solve 1,
\(\begin{align}
\mathbb{E}_{\pi}[R_{t+1} | S_t = s, A_t = a] &= \sum_r r p(R_{t+1} = r | S_t = s, A_t = a) \\
&= \sum_r \sum_{s'} rp(s', r | s, a) \\
\end{align}\)
Solve 2,
\(\begin{align}
\mathbb{E}_{\pi}[\gamma G_{t+1} | S_t = s, A_t = a] &= \sum_{s'} \mathbb{E}_{\pi}[\gamma G_{t+1} | S_t = s, S_t = s'] p(s' | s, a)\\
&= \sum_{a'} \sum_{s'} \mathbb{E}_{\pi}[\gamma G_{t+1} | S_t = s', A_t = a'] \pi(a'|s') p(s' | s, a) \\
&= \sum_{a'} \sum_{s'} \gamma q_\pi(s', a') \pi(a'|s') p(s' | s, a) \\
&= \sum_{s'} \sum_{r} p(s', r | s, a) \sum_{a'} \gamma q_\pi(s', a') \pi(a'|s') \\
\end{align}\)
Combining both equations give,
\(\begin{align}
\mathbb{E}_{\pi}[R_{t+1} | S_t = s, A_t = a] &+ \mathbb{E}_{\pi}[\gamma G_{t+1} | S_t = s, A_t = a] \\ &= \sum_r \sum_{s'} rp(s', r | s, a) + \sum_{s'} \sum_{r} p(s', r | s, a) \sum_{a'} \gamma q_\pi(s', a') \pi(a'|s') \\
&= \sum_r \sum_{s'} p(s', r | s, a) \left[r + \sum_{a'} \gamma q_\pi(s', a') \pi(a'|s') \right] \\
&= \sum_r \sum_{s'} p(s', r | s, a) \left[r + \gamma v_\pi(s') \right] \\
\end{align}\)
Thus, $v_\pi(s)$ is,
\(\begin{align}
&= \sum_a \pi(a|s) \sum_{s'} \sum_r p(s', r| s, a)\left[r + \gamma v_\pi(s') \right]
\end{align}\)
This is the Bellman equation for $v_\pi$.
Optimal Policies and Optimal Value Functions
A policy $\pi$ is defined to be better than or equal to a policy $\pi’$ if its expected return is greater than or equal to the expected return of $\pi’$ for all states. In other words, $\pi \geq \pi’$ if and only if $v_\pi(s) \geq v_\pi’(s)$ for all $s \in \mathcal{S}$. There is always one policy which is better than or equal to all other policies. This is called the optimal policy. There could be more than one optimal policy, and we denote them as $\pi_\star$. They share the same state-value function, called the optimal state-value function, denoted $v_\star$, and is defined as:
\[v_\star(s) \: \dot{=} \: \max_\pi \: v_\pi(s), \forall s \in \mathcal{S}\]Optimal policies also share the same optimal action-value function, denoted $q_\star$, and is defined as:
\[q_\star(s, a) \: \dot{=} \: \max_\pi \: q_\pi(s, a), \forall a \in \mathcal{A}, s \in \mathcal{S}\]For the state-action pair (s, a), this function gives the expected return for taking action a in state s and thereafter following an optimal policy. Thus we can write $q_\star$ in terms of $v_\star$ as:
\[q_\star(s, a) = \mathbb{E}_{\pi}[R_{t+1} + \gamma v_\star(S_{t+1})| S_t = s, A_t = a]\]$v_\star$’s condition can be written in a special form without reference to any policy. This is called the Bellman equation for $v_\star$, or the Bellman optimality equation. Intuitively, the Bellman optimality equation expresses the fact that value of a state under an optimal policy must equal the expected return for the best action from that state:
\[\begin{align} v_\star(s) &= \max_a \mathbb{E}[R_{t+1} + \gamma v_\star(S_{t+1})| S_t = s, A_t = a] \\ &=\max_a \sum_{s', r}p(s', r|s, a) \left[r + \gamma v_\star(s') \right] \end{align}\]These two equations are two forms of the Bellman optimality equation for $v_\pi$. The Bellman optimality equation for $q_\pi$ is:
\[\begin{align} q_\star(s, a) &= \mathbb{E}[R_{t+1} + \gamma \max_a q_\star(S_{t+1}, a')| S_t = s, A_t = a] \\ &= \sum_{s', r}p(s', r|s, a) \left[r + \gamma \max_a q_\star(s', a') \right] \end{align}\]We can explicitly solve the Bellman optimality equation to find an optimal policy. But this approach is rarely useful. This solution relies on at least three assumptions that are rarely true in practice:
- We accurately knows the dynamics of the environment.
- We have enough computational resources to complete the computation of the solution.
- Markov property
Problems
- Devise three example tasks of your own that fit into the MDP framework, identifying for each itsstates, actions, and rewards. Make the three examples as different from each other as possible.The framework is abstract and flexible and can be applied in many different ways. Stretch its limits in some way in at least one of your examples.
- Board games
- states: Current state of the board
- actions: Move to the next situation(eg: moving a chess piece)
- rewards: +1 for winning, -1 for losing, 0 for tie
- Driving car to a destination(one direction)
- states: Coordinates of the car, the speed of the car, and the distance to the destination
- actions: Accelerate, Brake, Turn left, Turn right
- rewards: +1 on reaching the destination, -1 on collision.
- Stock market
- states: Current price of the stock, balance, previous price, return on investment.
- actions: Buy, Sell, Hold
- rewards: +1 for each profit, -1 for each loss
- Board games
-
Is the MDP framework adequate to usefully represent all goal-directed learning tasks? Can you think of any clear exceptions?
Some times it will be hard to choose the proper reward for each action. And this will also fail when the state cannot be fully observed.
-
Consider the problem of driving. You could define the actions in terms of the accelerator, steering wheel, and brake, that is, where your body meets the machine. Or you could define them farther out—say, where the rubber meets the road, considering your actions to be tire torques. Or you could define them farther in—say, where your brain meets your body, the actions being muscle twitches to control your limbs. Or you could go to a really high level and say that your actions are your choices of where to drive. What is the right level, the right place to draw the line between agent and environment? On what basis is one location of the line to be preferred over another? Is there any fundamental reason for preferring one location over another, or is it a free choice?
We should draw a line on where it is less complex in space, and less computation. The most important thing is that if we can achieve the goal. But even then all or the hierarchy above plays some kind of role, since when it comes to real life all the above mentioned levels are really important.
-
Give a table analogous to that in Example 3.3, but for $p(s’,r|s, a)$. It should have columns for $s,a,s’,r$, and $p(s’,r|s, a)$, and a row for every 4-tuple for which $p(s’,r|s, a)>0$.
$s$ $a$ $s’$ $r$ $p(s’,r|s, a)$ high search high $r_{search}$ $\alpha$ high search low $r_{search}$ 1-$\alpha$ low search high -3 $\beta$ low search low $r_{search}$ 1-$\beta$ high wait high $r_{wait}$ 1 low wait low $r_{wait}$ 1 low recharge high 0 1 -
The equations in Section 3.1 are for the continuing case and need to be modified (very slightly) to apply to episodic tasks. Show that you know the modifications needed by giving the modified version of (3.3).
\[\begin{align} \underset{s' \in \mathcal{S^+}}{\sum} \underset{r \in \mathcal{R}}{\sum} p(s', r | s, a) = 1, \forall s \in \mathcal{S^+}, a \in \mathcal{A}(s) \end{align}\]where, $S^+$ denotes all states including the terminal state.
-
Suppose you treated pole-balancing as an episodic task but also used discounting, with all rewards zero except for -1 upon failure. What then would the return be at each time? How does this return differ from that in the discounted, continuing formulation of this task?
For the episodic case, the return is: $-\gamma^{k-t}$, where $k$ is the timestep at which task fails or in other word the end of episode.
For the continuing case, the return is: $-\underset{k \in K}{\sum} \gamma^{k-1}$, where $K$ is the set of all timesteps where the task fails.
-
Imagine that you are designing a robot to run a maze. You decide to give it a reward of +1 for escaping from the maze and a reward of zero at all other times. The task seems to break down naturally into episodes—the successive runs through the maze—so you decide to treat it as an episodic task, where the goal is to maximize expected total reward (3.7). After running the learning agent for a while, you find that it is showing no improvement in escaping from the maze. What is going wrong? Have you effectively communicated to the agent what you want it to achieve?
The problem with this approach is that regardless of how much time it takes, agent recieves same reward +1 on escape. Negative reward on increasing of the time steps might help in exiting the maze faster.
-
Suppose $\gamma$ = 0.5 and the following sequence of rewards is received $R_1 = 1, R_2 = 2, R_3 = 6, R_ 4= 3$, and $R_5 = 2$, with $T = 5$. What are $G_0, G_1, \dots , G_5$? Hint: Work backwards.
We know $G_t = R_{t+1} \gamma G_{t+1}$
$G_5 = 0$
$G_4 = R_5 = 2$
$G_3 = R_4 + \gamma G_4 = 3 + 0.5 * 2 = 4$
$G_2 = R_3 + \gamma G_3 = 6 + 0.5 * 4 = 8$
$G_1 = R_2 + \gamma G_2 = 2 + 0.5 * 8 = 6$
$G_0 = R_1 + \gamma G_1 = -1 + 0.5 * 6 = 2$ -
Suppose $\gamma = 0.9$ and the reward sequence is $R_1 = 2$ followed by an infinite sequence of 7s. What are $G_1$ and $G_0$?
\(\begin{align} G_1 &= R_{2} + 0.9 G_1 + 0.9^2 G_2 + 0.9^3 G_3 + \dots \\ &= 7 + 0.9*7 + 0.9^2*7 + 0.9^3*7 + \dots \\ &= \frac{7}{1-0.9} \\ &= 70 \end{align}\)$G_0 = R_1 + 0.9 G_1 = 2 + 0.9*70 = 72$
-
Prove the second equality in (3.10)
Given $\gamma < 1$, and reward is a constant +1.
\(\begin{align} G_t &= R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \dots \\ &= 1 + \gamma * 1 + \gamma^2 * 1 + \dots \\ &= \gamma^0 + \gamma^1 + \gamma^2 + \dots \\ &= \sum_{i=0}^{\infty} \gamma^i \\ &= \frac{1}{1-\gamma} \end{align}\) -
If the current state is $S_t$, and actions are selected according to stochastic policy $\pi$, then what is the expectation of $R_{t+1}$ in terms of $\pi$ and the four-argument function p(3.2)?
We have to find $\mathbb{E}[R_t | S_t]$. We know that:
\[\begin{align} \mathbb{E}[R_{t+1} | A_t, S_t] = \sum_r \sum_s p(s', r| s, a)r \\ \end{align}\]Here, action is selected according to stochastic policy $\pi$. According to Law of total expectation, $\mathbb{E}[\mathbb{E}[X | Y_2] | Y_1] = \mathbb{E}[X | Y_1]$. Using this law we can write the following equation:
\[\begin{align} \mathbb{E}[R_{t+1} | S_t] = \mathbb{E}_{A_t \sim \pi}[\mathbb{E}[R_{t+1} |A_t, S_t] | S_t] \end{align}\]So,
\[\begin{align} \mathbb{E}_{A_t \sim \pi}[\mathbb{E}[R_{t+1} |A_t, S_t] | S_t] = \sum_a \pi(a|s) \sum_r \sum_s p(s', r | s, a)r \\ \end{align}\] -
Give an equation for $v_\pi$ in terms of $q_\pi$ and $\pi$.
We can use the Law of Total Expectation here,
\[\begin{align} v_\pi &= \mathbb{E}_{\pi}[G_t | S_t] \\ &= \sum_a \mathbb{E}_{\pi}[G_t | S_t = s, A_t= a]p(A_t = a|S_t = s) \\ &= \sum_a q_\pi(s, a) \pi(a|s) \\ \end{align}\] -
Give an equation for $q_\pi$ in terms of $v_\pi$ and the four-argument $p$.
\[\begin{align} q_\pi(s, a) &= \mathbb{E}_{\pi}[G_t | S_t = s, A_t = a] \\ &= \mathbb{E}_{\pi}[R_{t+1} + \gamma G_{t+1} | S_t = s, A_t = a] \\ &= \mathbb{E}_{\pi}[R_{t+1} | S_t = s, A_t = a] + \mathbb{E}_{\pi}[\gamma G_{t+1} | S_t = s, A_t = a] \\ \end{align}\]Diving the equations, into part:
- $\mathbb{E}_{\pi}[R_{t+1} | S_t = s, A_t = a]$
- $\mathbb{E}_{\pi}[\gamma G_{t+1} | S_t = s, A_t = a]$
Solve 1,
\(\begin{align} \mathbb{E}_{\pi}[R_{t+1} | S_t = s, A_t = a] &= \sum_r r p(R_{t+1} = r | S_t = s, A_t = a) \\ &= \sum_r \sum_{s'} rp(s', r | s, a) \\ \end{align}\)Solve 2,
\(\begin{align} \mathbb{E}_{\pi}[\gamma G_{t+1} | S_t = s, A_t = a] &= \sum_{s'} \mathbb{E}_{\pi}[\gamma G_{t+1} | S_t = s, S_t = s'] p(s' | s, a)\\ &= \sum_{a'} \sum_{s'} \mathbb{E}_{\pi}[\gamma G_{t+1} | S_t = s', A_t = a'] \pi(a'|s') p(s' | s, a) \\ &= \sum_{a'} \sum_{s'} \gamma q_\pi(s', a') \pi(a'|s') p(s' | s, a) \\ &= \sum_{s'} \sum_{r} p(s', r | s, a) \sum_{a'} \gamma q_\pi(s', a') \pi(a'|s') \\ \end{align}\)Combining both equations,
\[\begin{align} q_\pi(s, a) &= \sum_r \sum_{s'} rp(s', r | s, a) + \sum_{s'} \sum_{r} p(s', r | s, a) \sum_{a'} \gamma q_\pi(s', a') \pi(a'|s') \\ &= \sum_r \sum_{s'} p(s', r | s, a) \left[r + \sum_{a'} \gamma q_\pi(s', a') \pi(a'|s') \right] \\ &= \sum_r \sum_{s'} p(s', r | s, a) \left[r + \gamma v_\pi(s') \right] \\ \end{align}\] -
The Bellman equation (3.14) must hold for each state for the value function $v_\pi$ shown in Figure 3.2 (right) of Example 3.5. Show numerically that this equation holds for the center state, valued at +0.7, with respect to its four neighboring states, valued at +2.3, +0.4, -0.4, and +0.7. (These numbers are accurate only to one decimal place.)
\[\begin{align} v_\pi(s) &= \sum_a \pi(a|s) \sum_r \sum_s p(s', r | s, a)\left[r + \gamma v_\pi(s') \right] \\ &= \frac{1}{4}(2.3\times 0.9) + \frac{1}{2} (0.4\times 0.9) + \frac{1}{4}(-0.4\times 0.9) + \frac{1}{4}(0.7\times 0.9) \\ &= 0.675 \approx 0.7 \\ \end{align}\] -
In the gridworld example, rewards are positive for goals, negative forrunning into the edge of the world, and zero the rest of the time. Are the signs of these rewards important, or only the intervals between them? Prove, using (3.8), that adding a constant c to all the rewards adds a constant,$v_c$, to the values of all states, and thus does not affect the relative values of any states under any policies. What is $v_c$ in terms of c and $\gamma$?
\[\begin{align} v_\pi(s) &= \mathbb{E}[G_t | S_t = s] \\ &= \mathbb{E}\left[\sum_{k=t+1}^\infty \gamma^{k-t-1} (R_k+c) \middle| S_t = s\right] \\ &= \mathbb{E}\left[\sum_{k=t+1}^\infty \gamma^{k-t-1} R_k + \sum_{k=t+1}^\infty \gamma^{k-t-1}c \middle| S_t = s\right] \\ &= \mathbb{E}\left[\sum_{k=t+1}^\infty \gamma^{k-t-1} R_k \middle| S_t = s\right] + \mathbb{E}\left[\sum_{k=t+1}^\infty \gamma^{k-t-1} c \middle| S_t = s\right] \\ &= \mathbb{E}\left[G_t \middle| S_t = s\right] + c\sum_{k=t+1}^\infty \gamma^{k-t-1}\\ &= v_\pi(s) + \frac{c}{1-\gamma}\\ \implies v_c = \frac{c}{1-\gamma}\\ \end{align}\]Adding a constant doesn’t affect the relative values of any state, thus the intervals between the rewards are important, and not the signs.
-
Now consider adding a constant c to all the rewards in an episodic task,such as maze running. Would this have any effect, or would it leave the task unchanged as in the continuing task above? Why or why not? Give an example.
\[\begin{align} v_\pi(s) &= \mathbb{E}[G_t | S_t = s] \\ &= \mathbb{E}\left[\sum_{k=t+1}^T \gamma^{k-t-1} (R_k+c) \middle| S_t = s\right] \\ &= \mathbb{E}\left[\sum_{k=t+1}^T \gamma^{k-t-1} R_k + \sum_{k=t+1}^T \gamma^{k-t-1}c \middle| S_t = s\right] \\ &= \mathbb{E}\left[\sum_{k=t+1}^T \gamma^{k-t-1} R_k \middle| S_t = s\right] + \mathbb{E}\left[\sum_{k=t+1}^T \gamma^{k-t-1} c \middle| S_t = s\right] \\ &= \mathbb{E}\left[G_t \middle| S_t = s\right] + c\sum_{k=t+1}^T \gamma^{k-t-1}\\ &= v_\pi(s) + \frac{c}{1-\gamma}\\ \implies v_c = \frac{c(1- \gamma^T)}{1-\gamma}\\ \end{align}\]Since, $\frac{c(1- \gamma^T)}{1-\gamma}$ depends on the number of time steps, does affect the agent.
for eg: Suppose a task with rewards 1 on reaching the goal and 0 otherwise. Suppose $\gamma = 0.9$. There was one task which took 2 time steps to complete, and another task which took 1 time step to complete. Thus reward for agent one is 0 + 0.9 * 1 and agent two is 1. But if we add a constant c = 2 to all the rewards, the reward for agent one is 2 + 0.9 * (1 + 2) and agent two is (1 + 2). This might cause agent, to collect intermediate rewards, and not reach the goal.
-
What is the Bellman equation for action values, that is, for $q_\pi$ ? It must give the action value $q_\pi(s, a)$ in terms of the action values,$q_\pi(s’,a’)$, of possible successors to the state–action pair $(s, a)$. Hint: the backup diagram to the right corresponds to this equation. Show the sequence of equations analogous to (3.14), but for actionvalues.
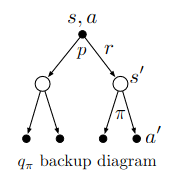
Steps are same as that in problem 13.
\(\begin{align} q_\pi(s, a) = \sum_r \sum_{s'} p(s', r | s, a) \left[r + \sum_{a'} \gamma q_\pi(s', a') \pi(a'|s') \right] \\ \end{align}\) -
The value of a state depends on the values of the actions possible in that state and on how likely each action is to be taken under the current policy. We can think of this in terms of a small backup diagram rooted at the state and considering each possible action:
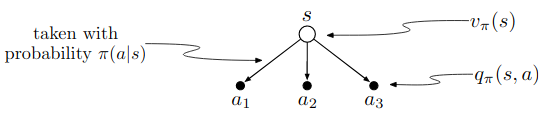
Give the equation corresponding to this intuition and diagram for the value at the root node,$v_\pi(s)$, in terms of the value at the expected leaf node, $q_\pi(s, a)$, given $S_t=s$. This equation should include an expectation conditioned on following the policy, $\pi$. Then give a second equation in which the expected value is written out explicitly in terms of $\pi(a|s)$ such that no expected value notation appears in the equation.1)
\(\begin{align} v_\pi &= \mathbb{E}_{\pi}[G_t | S_t] \\ &= \mathbb{E}_{\pi}[\mathbb{E}_{\pi}[G_t | S_t = s, A_t = a]|S_t = s] \\ &= \mathbb{E}_{\pi}[q_\pi(s,a) |s] \\ \end{align}\)2)
\(\begin{align} v_\pi &= \mathbb{E}_{\pi}[G_t | S_t] \\ &= \sum_a \mathbb{E}_{\pi}[G_t | S_t = s, A_t= a]p(A_t = a|S_t = s) \\ &= \sum_a q_\pi(s, a) \pi(a|s) \\ \end{align}\) -
The value of an action, $q_\pi(s, a)$, depends on the expected next reward and the expected sum of the remaining rewards. Again we can think of this in terms of a small backup diagram, this one rooted at an action (state–action pair) and branching to the possible next states:
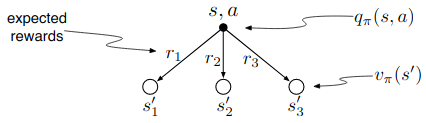
Give the equation corresponding to this intuition and diagram for the action value, $q_\pi(s, a)$, in terms of the expected next reward, $R_{t+1}$, and the expected next state value, $v_\pi(S_{t+1})$, given that $S_t = s$ and $A_t = a$. This equation should include an expectation but not one conditioned on following the policy. Then give a second equation, writing out the expected value explicitly in terms of $p(s’,r|s, a)$ defined by (3.2), such that no expected value notation appears in the equation.1)
\(\begin{align} q_\pi(s,a) &= \mathbb{E}_{\pi}[R_t + \gamma G_{t+1} | S_t, A_t] \\ &= \mathbb{E}_{\pi}[R_t | S_t = s, A_t = a] + \gamma \mathbb{E}_{\pi}[G_{t+1} | S_t = s, A_t = a] \\ &= \mathbb{E}_{\pi}[R_t | S_t = s, A_t = a] + \gamma \mathbb{E}_{\pi}[\mathbb{E}_{\pi}[G_{t+1} | S_{t+1} = s' ]| S_t = s, A_t = a] \\ &= \mathbb{E}_{\pi}[R_t + \gamma \mathbb{E}_{\pi}[G_{t+1} | S_{t+1} = s' ]| S_t = s, A_t = a] \\ &= \mathbb{E}_{\pi}[R_t + \gamma v_\pi(s')| S_t = s, A_t = a] \\ \end{align}\)2)
\(\begin{align} q_\pi(s,a) &= \sum_r \sum_{s'} p(s', r | s, a) \left[r + \gamma v_\pi(s') \right] \\ \end{align}\)proof for the second equation is in problem 13.
-
Draw or describe the optimal state-value function for the golf example.
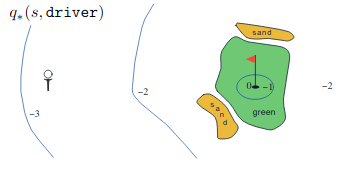
The optimal state-value function for this case is equal to $q_\star(s, driver)$ everywhere except for the green area(driver covers more distance than putter). And in green area its better to use the putter. $q_\star(s, driver)$ gives the value of using the driver first and then whatever is better.
-
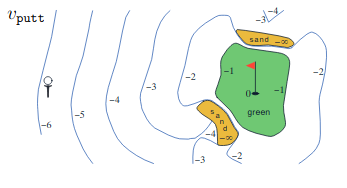
Draw or describe the contours of the optimal action-value function for putting, $q_\star(s,putter)$, for the golf example
The optimal action-value function is same as state value for putter.
-
Consider the continuing MDP shown on to the right. The only decision to be made is that in the top state, where two actions are available,left and right.The numbers show the rewards that are received deterministically aftereach action. There are exactly two deterministic policies,$\pi_{left}$ and $\pi_{right}$. What policy is optimal if $\gamma $= 0? If $\gamma$ = 0.9? If $\gamma$ = 0.5?
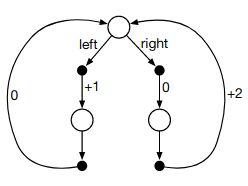
We know $v_\pi(s) = \mathbb{E}_{\pi}[G_t | S_t = s]$.
-
$\gamma = 0$
For $\pi_{left}, v_\pi(s) = \mathbb{E}[1 + 0*0] = 1$For $\pi_{right}$, $v_\pi(s)$ = $\mathbb{E}[0 + 0*2] = 0$
So, $\pi_{left}$ is optimal.
-
$\gamma = 0.9$
For $\pi_{left}, v_\pi(s) = \mathbb{E}[1 + 0.9*0] = 1$For $\pi_{right}$, $v_\pi(s)$ = $\mathbb{E}[0 + 0.9*2] = 1.8$
So, $\pi_{right}$ is optimal.
-
$\gamma = 0.5$
For $\pi_{left}, v_\pi(s) = \mathbb{E}[1 + 0.5*0] = 1$For $\pi_{right}$, $v_\pi(s)$ = $\mathbb{E}[0 + 0.5*2] = 1$
So, both $\pi_{left}$ and $\pi_{right}$ are optimal.
-
-
Give the Bellman equation for $q_\star$ for the recycling robot.
\[\begin{align} &q_{*}(h,s) = \alpha \left( r_{search} + \gamma \max_{a'}q_{*}(h,a')\right) + \left(1 - \alpha\right) \left(r_{search} + \gamma \max_{a'}q_{*}\left(l, a'\right)\right) \\ &q_{*}(l,s) = \left(1-\beta\right)\left(-3 + \gamma \max_{a'}q_{*}(h,a')\right) + \beta\left(r_{search} + \gamma \max_{a'}q_{*}(l,a')\right) \\ &q_{*}(h,w) = \left(r_{wait} + \gamma \max_{a'}q_{*}(h,a')\right) \\ &q_{*}(l,w) = \left(r_{wait} + \gamma \max_{a'}q_{*}(l,a')\right) \\ &q_{*}(l,re) = \left(0 + \gamma \max_{a'}q_{*}(h,a')\right) \\ \end{align}\] -
Figure 3.5 gives the optimal value of the best state of the gridworld as 24.4, to one decimal place. Use your knowledge of the optimal policy and (3.8) to express this value symbolically, and then to compute it to three decimal places.
A -> A’ -> A
\[\begin{align} G_t &= 10\gamma^0 + 0\gamma^1 + 0\gamma^2 + 0\gamma^3 + 0\gamma^4 + 10\gamma^5 + \dots \\ &= 10\gamma + 10\gamma^5 + 10\gamma^10 + \dots + 10(\gamma^5)^\infty \\ &= \frac{10}{1 - \gamma^5} \\ &= 24.419, \because \gamma = 0.9 \end{align}\] -
Give an equation for $v_\star$ in terms of $q\star$.
$v_\star(s) = \max_a q_\star(s,a)$
-
Give an equation for $q_\star$ in terms of $v_\star$ and the four-argument p.
$q_\star(s,a) = \max_a \sum_{s’, r}p(s’, r | s, a) \left[r + \gamma v_\star(s’) \right]$
-
Give an equation for $\pi_\star$ in terms of $q_\star$.
$\pi_\star(a|s) = \arg\max_a q_\star(s,a)$
-
Give an equation for $\pi_\star$ in terms of $v_\star$ and the four-argument p.
$\pi_\star(a|s) = \arg\max_a \sum_{s’, r}p(s’, r | s, a) \left[r + \gamma v_\star(s’) \right]$
-
Rewrite the four Bellman equations for the four value functions ($v_\star$, $v_\pi$ , $q_\star$, and $q_\pi$) in terms of the three argument function p(3.4)and the two-argument function r(3.5).
- $v_\pi(s) = \sum_a \pi(a|s) \sum_{s’} p(s’ | s, a)[r(s,a) + v_\pi(s’)]$
- $v_\star(s) = \max_a \sum_{s’} p(s’ | s, a)[r(s,a) + v_\pi(s’)]$
- $q_\pi(s,a) = \sum_{s’} p(s’, r | s, a) \left[r(s,a) + \gamma v_\pi(s’) \right]$
- $q_\star(s,a) = \sum_{s’} p(s’, r | s, a) \left[r(s,a) + \gamma \max_{a’} q_\pi(s’,a’) \right]$
- $v_\pi(s) = \sum_a \pi(a|s) \sum_{s’} p(s’ | s, a)[r(s,a) + v_\pi(s’)]$