Temporal-Difference learning is a combination of the MC ideas and DP ideas. TD methods can learn directly from raw experiences like MC methods and updates estimates based in part on other learned estimates, without waiting for a final outcome(they bootstrap) like DP methods.

TD prediction

Both Monte Carlo and TD use experience to solve the prediction problem. Monte Carlo methods wait until the return following as visit is known, and then use the return as a target for $V(S_t)$. A simple case of MC:

\[V(S_t) \leftarrow V(S_t) + \alpha \left[G_t - V(S_t) \right],\]

where $G_t$ is the actual return following time $t$, and $\alpha$ is a constant step-size parameter. Whereas MC methods wait until the episode to determine the increment to $V(S_t)$, TD methods need to wait only until the next time step. At time $t+1$ they immediately form a target and make update using the observed reward $R_{t+1}$ and the estimated value $V(S_{t+1})$. The simplest TD method makes the update

\[V(S_t) \leftarrow V(S_t) + \alpha \left[R_{t+1} + \gamma V(S_{t+1}) - V(S_t) \right],\]

immediately on transition to $S_{t+1}$ and receiving $R_{t+1}$. In effect, the target for the Monte Carlo update is $G_t$, whereas the target is $R_{t+1} + \gamma V(S_{t+1})$ for TD update. This method is called $TD(0)$, or one step TD. This is special case of the $TD(\lambda)$. $TD(0)$ is a bootstrapping method (because it updates based on an exisiting estimate), like DP.

Tabular TD(0) for estimating $v_\pi$

Tabular TD(0) for estimating $v_\pi$
  • Input: the policy $\pi$ to be evaluated
  • Algorithm parameter: step size $\alpha \in (0,1]$
  • Initialize $V(S)$, for all $s \in \mathcal{S}^+$, arbitrarily except that $V(terminal) = 0$
  • Loop for each episode:
    • Initialize $S$
    • Loop for each step of episode:
      • $A \leftarrow$ action given by $\pi$ for $S$
      • Take action $A$, observe $R$, $S'$
      • $V(S) \leftarrow$ $V(S) + \alpha \left[R + \gamma V(S') - V(S) \right]$
      • $S \leftarrow$ $S'$
    • until $S$ is terminal

    • The quantity in the brackets of $TD(0)$ update is a sort of error, measuring the difference between the estimated value of $S_t$ and the better estimate $R_{t+1} + \gamma V(S_{t+1})$. The quantity is called as $TD$ error.

    \[\delta_t\:\dot{=}\:R_{t+1} + \gamma V(S_{t+1}) - V(S_t)\]

    The TD error at each time is the error in the estimate made at that time. The TD error will be available only in the next step since it depends on the next state and next reward. That is, $\delta_t$ is the error in $V(S_t)$, available at time $t+1$. If the array $V$ does not change during the episode (like MC methods), then Monte Carlo error can be writtern as a sum of TD errors.

    \[\begin{align} G_t - V(S_t) &= R_{t+1} + \gamma G_{t+1} - V(S_t) \\ &= R_{t+1} + \gamma G_{t+1} - V(S_t) + \gamma V(S_{t+1}) - \gamma V(S_{t+1})\\ &= \delta_t + \gamma(G_{t+1} - V(S_{t+1})) \\ &= \delta_t + \gamma \delta_{t+1} + \gamma^2 (G_{t+2} - V(S_{t+2})) \\ &= \delta_t + \gamma \delta_{t+1} + \gamma^2 \delta_{t+2} + \cdots + \gamma^{T-t-1} \delta_{T-1} + \gamma^{T-t}(G_T - V(S_T)) \\ &= \delta_t + \gamma \delta_{t+1} + \gamma^2 \delta_{t+2} + \cdots + \gamma^{T-t-1} \delta_{T-1} + \gamma^{T-t}(0 - 0), \quad G_T, V(S_T)\text{ is 0 (terminal state)} \\ &= \sum_{k=t}^{T-1}\gamma^{k-t} \delta_k \end{align}\]

    This identity is not exact if $V$ is updated during the episode, but if the step size is small then it may still hold approximately.

    Advantages of TD Prediction Methods

    TD methods update their estimates based in part on other estimates. They learn a guess from a guess - they bootstrap. TD methods always have an advantage over DP methods, since it doesnt require a model of the environment, of its reward and next-state probability. The advantage of TD methods over MC method is that they are naturally implemented online and fully incremental. While we wait for a whole episode in MC methods, we only have to wait for one time step in TD. There are problems which are very long and some other may be continuous and have no episodes. Some MC methods must ignore or discount episodes on which experimental actions are taken, which greatly affects learning speed. TD methods are much less susceptible to these problems because they learn regardelss of what actions are taken.

    For any fixed policy $\pi$, TD(0) has been proved to converge to $v_\pi$, in the mean for a constant step-size parameter if it is sufficiently small, and with probability 1 if the step-size parameter decreases according to the usual stochastic approximation condition. Usually TD methods converge faster than constant-$\alpha$ methods on stochastic tasks.

    Optimality of TD(0)

    Suppose there is only finite amount of experience. In this case, a common approach with incremental learning methods is to present the experience repeatedly until the method converges. Given an approximate value function, $V$, the increments are computed for every time step $t$ at which a non-terminal state is visited, but value function is changed only once, by the sum of all increments. Then all available experience is processed again with new value function to produce overall increment, and so on, until the value function converges. We call this batch updating because updates are made only after processing each complete batch of training data.

    Under batch-updating, TD(0) converges deterministically to a single answer independently of the step size parameter, as long as $\alpha$ is sufficiently small. Constant-$\alpha$ MC method also converges, but to a different answer.

    Sarsa: On-policy TD Control

    The first step is to learn an action function rather than a state-value function. In particular, for an on-policy method we must estimate $q_\pi(s,a)$ for the current behavior policy $\pi$ and for all states $s$ and actions $a$. This can be done using the TD methods for learning $v_\pi$. The update is:

    \[Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha \left[R_{t+1} + \gamma Q(S_{t+1}, A_{t+1}) - Q(S_t, A_t) \right]\]

    This update is done after every transition from non-terminal state $S_t$. If $S_{t+1}$ is terminal, then Q(S_{t+1}, A_{t+1}) is defined as $0$. This rule uses every elements of the quintuple of events, (S_t, A_t, R_{t+1}, S_{t+1}, A_{t+1}), that makes a transition from one state-action pair to another. This quintuple gives rise to the name Sarsa.

    The convergence properties of the Sarsa algorithm depend on the nature of the policy’s dependence on Q. Sarsa converges with probability 1 to an optimal policy and action-value function as long as all state-action pairs are visited an infinite number of times and policy converges in the limit of the greedy policy.

    Pseudocode: Sarsa (on-policy TD control)

    Sarsa (on-policy TD control) for estimating $Q \approx q_\star$
  • Algorithm parameters: step size $\alpha \in (0, 1]$, small $\epsilon > 0$
  • Initialize $Q(s, a)$, for all $s \in \mathcal{S}^+, a \in \mathcal{A}(s)$, arbitrarily except that $Q(terminal, .) = 0$
  • Loop for each episode:
    • Initialize $S$
    • Choose $A$ from $S$ using policy derived from $Q$ (eg. $\epsilon$-greedy)
    • Loop for each step of episode:
      • Take action $A$, observe $R, S'$
      • Choose $A'$ from $S'$ using policy derived from $Q$ (eg. $\epsilon$-greedy)
      • $Q(S,A) \leftarrow Q(S,A) + \alpha \left[R + \gamma Q(S',A') - Q(S,A) \right]$
      • $S \leftarrow S'; A \leftarrow A'$
    • until S is terminal

    • Q-Learning: Off-policy TD Control

    This is the off-policy TD control algorithm. It is defined by

    \[Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha \left[R_{t+1} + \gamma \max_a Q(S_{t+1}, a) - Q(S_t, A_t) \right]\]

    In this case, the learned action-value function, $Q$, directly approximates $q_\star$, the optimal action-value function, independent of the policy begin followed. Under the assumption that all pairs are updated continuously and a variant of the usual stochastic approximation conditions on the sequence of step-size parameters $Q$, has been shown to converge with probability 1 to $q_\star$.

    Pseudocode: Q-Learning (off-policy TD control)

    Q-Learning (off-policy TD control) for estimating $\pi \approx \pi_\star$
  • Algorithm parameters: step size $\alpha \in (0, 1]$, small $\epsilon > 0$
  • Initialize $Q(s, a)$, for all $s \in \mathcal{S}^+, a \in \mathcal{A}(s)$, arbitrarily except that $Q(terminal, .) = 0$
  • Loop for each episode:
    • Initialize $S$
    • Loop for each step of episode:
      • Choose $A$ from $S$ using policy derived from $Q$(eg. $\epsilon$-greedy)
      • Take action $A$, observe $R, S'$
      • $Q(S,A) \leftarrow Q(S,A) + \alpha \left[R + \gamma \max_a Q(S', a) - Q(S,A) \right]$
      • $S \leftarrow S'$
    • until S is terminal

    • Expected Sarsa

    This is a learning algorithm which is similar to $Q$-learning, but instead of the maximum over next state-action pair it uses the expected value, taking into account how likely each action is under the current policy. That is, the update is

    \[\begin{align} Q(S_t, A_t) &\leftarrow Q(S_t, A_t) + \alpha \left[R_{t+1} + \gamma \mathbb{E}_\pi[Q(S_{t+1}, A_{t+1}) | S_{t+1}] - Q(S_t, A_t) \right] \\ &\leftarrow Q(S_t, A_t) + \alpha \left[R_{t+1} + \gamma \sum_a \pi(a | S_{t+1}) Q(S_{t+1}, a) - Q(S_t, A_t) \right] \end{align}\]

    but otherwise follows the schema of $Q$-learning. Given the next state $S_{t+1}$, this algorithm moves deterministically in the same direction as Sarsa moves in expectation, and accordingly it is called expected Sarsa.

    Expected Sarsa is more complex computationally than Sarsa, but in return, it eliminates the variance due to the random selection of $A_{t+1}$.

    Maximization Bias and Double Learning

    All control algorithms discussed until now involves maximization in the construction of their target policies. In these algorithms, a maximum over estimated values is used implcitly as an estimate of the maximum value which can lead to a significant positive bias. For example, consider a true value $q(s, a)$ with maximum of 0 but whose estimated values $Q(s, a)$, are uncertain and thus distributed some above and some below zero. The maximum of the true values are zero, but maximum of estimates is positive, a positive bias. We call this maximization bias.

    One way to view maximization bias is that, it is due to using the same samples both to determine the maximizing action and to estimate its value. Suppose we divided the plays in two sets and used them to learn two independent estimates, say $Q_1(a)$ and $Q_2(a)$, each an estimate of true value $q(a)$, for all $a \in \mathcal{A}$. We could use estimate $Q_1$ to determine the maximizing action $A^\star = \arg\max_a Q_1(a)$, and the $Q_2$ to provide the estimate of its value, $Q_2(A^\star) = Q_2(\arg\max_a Q_1(a))$. This estimate will hten be unbiased in the sense that $\mathbb{E}[Q_2(A^\star)] = q(A^\star)$. We can also repeat the process with role of two estimates reversed to yield a second unbiased estimate $Q_1(\arg\max_a Q_2(a))$. This is the idea of Double Learning. The update is

    \[Q_1(S_t, A_t) \leftarrow Q_1(S_t, A_t) + \alpha \left[R_{t+1} + \gamma Q_2(S_{t+1}, \arg\max_a Q_1(S_{t+1}, a)) - Q_1(S_t, A_t) \right]\]

    Pseudocode: Double Q-Learning

    Double Q-Learning, for estimating $Q_1 \approx Q_2 \approx q_\star$
  • Algorithm parameters: step size $\alpha \in (0, 1]$, small $\epsilon > 0$
  • Initialize $Q_1(s, a)$ and $Q_2(s, a)$, for all $s \in \mathcal{S}^+, a \in \mathcal{A}(s)$, arbitrarily except that $Q(terminal, .) = 0$
  • Loop for each episode:
    • Initialize $S$
    • Loop for each step of episode:
      • Choose $A$ from $S$ using pthe policy $\epsilon$-greedy in $Q_1 + Q_2$
      • Take action $A$, observe $R, S'$
      • With 0.5 probability:
        • $Q_1(S,A) \leftarrow Q_1(S,A) + \alpha \left[R + \gamma Q_2(S', \arg\max_a Q_1(S', a)) - Q_1(S,A) \right]$
      • else:
        • $Q_2(S,A) \leftarrow Q_2(S,A) + \alpha \left[R + \gamma Q_1(S', \arg\max_a Q_2(S', a)) - Q_2(S,A) \right]$
      • $S \leftarrow S'$
    • until S is terminal

    • Problems

    1. If $V$ changes during the episode, then (6.6) only holds approximately; what would the difference be between the two sides? Let $V_t$ denote the array of state values used at time $t$ in the TD error (6.5) and in the TD update (6.2). Redo the derivation above to determine the additional amount that must be added to the sum of TD errors in order to equal the Monte Carlo error.

      \[\begin{align} G_t - V(S_t) &= R_{t+1} + \gamma G_{t+1} - V_t(S_t) \\ &= R_{t+1} + \gamma G_{t+1} - V_t(S_t) + \gamma V_t(S_{t+1}) - \gamma V_t(S_{t+1})\\ &= \delta_t + \gamma(G_{t+1} - V_t(S_{t+1})) \\ &= \delta_t + \gamma(G_{t+1} - [V_{t+1}(S_{t+1}) + \alpha[R_{t+2} + \gamma V_t(S_{t+2}) - V_t(S_{t+1})]]) \\ &= \delta_t + \gamma(G_{t+1} - V_{t+1}(S_{t+1})) + \gamma \alpha[R_{t+2} + \gamma V_t(S_{t+2}) - V_t(S_{t+1})] \\ &= \delta_t + \gamma(G_{t+1} - V_{t+1}(S_{t+1})) + \gamma \rho_{t+1} \\ &= \delta_t + \gamma \delta_{t+1} + \gamma^2(G_{t+2} - V_{t+2}(S_{t+1})) + \gamma \rho_{t+1} + \gamma^2 \rho_{t+2} \\ &= \delta_t + \gamma \delta_{t+1} + \gamma^2 \delta_{t+2} + \cdots + \gamma^{T-t-1} \delta_{T-1} + \gamma^{T-t}(G_T - V_T(S_T)) + \gamma \rho_{t+1} + \gamma^2 \rho_{t+2} + \cdots + \gamma^{T-t} \rho_{T-t-1} \\ &= \delta_t + \gamma \delta_{t+1} + \gamma^2 \delta_{t+2} + \cdots + \gamma^{T-t-1} \delta_{T-1} + \gamma^{T-t}(0 - 0) + \gamma \rho_{t+1} + \gamma^2 \rho_{t+2} + \cdots + \gamma^{T-t} \rho_{T-t-1} \\ &= \sum_{k=t}^{T-1}\gamma^{k-t} \delta_k + \sum_{k=t}^{T-1}\gamma^{k-t+1} \rho_{k+1} \\ &= \sum_{k=t}^{T-1}\gamma^{k-t} \delta_k + \sum_{k=t}^{T-1}\gamma^{k-t+1} \alpha[R_{k+2} + \gamma V_{k}(S_{k+2}) - V_{k}(S_{k+1})] \\ \end{align}\]

    2. This is an exercise to help develop your intuition about why TD methods are often more efficient than Monte Carlo methods. Consider the driving home example and how it is addressed by TD and Monte Carlo methods. Can you imagine a scenario in which a TD update would be better on average than a Monte Carlo update? Givean example scenario — a description of past experience and a current state — in which you would expect the TD update to be better. Here’s a hint: Suppose you have lots of experience driving home from work. Then you move to a new building and a new parking lot (but you still enter the highway at the same place). Now you are starting to learn predictions for the new building. Can you see why TD updates are likely to be much better, at least initially, in this case? Might the same sort of thing happen in the original scenario?

      TD update is better since we don’t need to change the highway part. MC on other hand bring average improvement to all the states, including highway which we don’t need. TD might be useful in cases where its hard to make terminal states.

    3. From the results shown in the left graph of the random walk example it appears that the first episode results in a change in only $V(A)$. What does this tell you about what happened on the first episode? Why was only the estimate for this one state changed? By exactly how much was it changed?

      Given $V(s) = 0 \forall s$, and $\alpha = 0.1$. We know that $V_{t+1}(S_t) \leftarrow V_t(S_t) + \alpha[R_{t+1} + \gamma V_t(S_{t+1}) - V_t(S_t)]$.

      Here to explain why the first episode only resulted in changing the value of state A, we have to look at the possible transition. By looking graph we can see that the value of state A decreased, which means that the episode ended at the left terminal state. Because, if it has to decrease, then the term $[R_{t+1} + \gamma V_t(S_{t+1}) - V_t(S_t)]$ is negative. We know $V_t(S_{t+1})$ and $V_t(S_t)$ are both 0.5 when transition from C to B. Similarly for B to A. But for A $V_t(S_{t+1})$ is zero, because it is terminal state. So,

      $V(A) = V(A) + \alpha[R_{t+1} + \gamma V(terminal) - V(A)]$
      $V(A) = 0.5 + 0.1[0 + 0 - 0.5]$
      $V(A) = 0.45$

    4. The specific results shown in the right graph of the random walk example are dependent on the value of the step-size parameter,$\alpha$. Do you think the conclusions about which algorithm is better would be affected if a wider range of $\alpha$ values were used? Is there a different, fixed value of $\alpha$ at which either algorithm would have performed significantly better than shown? Why or why not?

      With high value of alpha, it may achieve faster convergence in the initial stage. But, with low value of alpha, it may be slower to converge, but it will reach more close to the optimal value than with a higher value of alpha.

    5. In the right graph of the random walk example, the RMS error of the TD method seems to go down and then up again, particularly at high $alpha$’s. What could have caused this? Do you think this always occurs, or might it be a function of how the approximate value function was initialized?

      With higher value of alpha, when update is done, there is a chance that it under/over-shoots the optimal value. Which causes error to go up. Then it does the correction which makes the error go down. And may repeat.

    6. In Example 6.2 we stated that the true values for the random walk example are 1/6, 2/6, 3/6, 4/6, and 5/6, for states $A$ through $E$. Describe at least two different ways that these could have been computed. Which would you guess we actually used? Why?

      We can use either

      1. Dynamic Programming

        Solve bellman equation $(I - \gamma P)v = R$, (Proof for the equation)



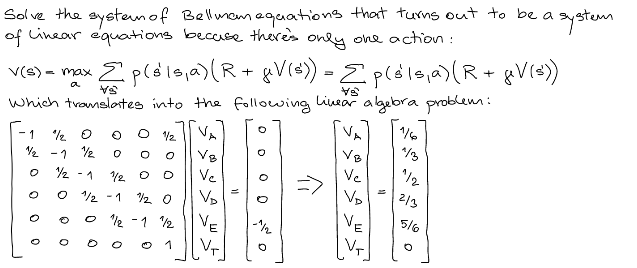
        This is the solution, here the equation is of form $-(I - \gamma P)v = -R$(to avoid confusion why terms on both side are negative).

      2. Monte Carlo method.

      For this case, Dynamic Programming would have been choosed because MC method needs more time to converge.

    7. Design an off-policy version of the TD(0) update that can be used with arbitrary target policy $\pi$ and covering behavior policy $b$, using at each step $t$ the importance sampling ratio $\rho_{t:t} (5.3).

      The update for TD(0) is:

      \[V(s) \leftarrow V(s) + \alpha[R_{t+1} + \gamma V(s') - V(s)]\]

      Since, what we have are samples from a different policy $b$, we will have to introduce importance sampling.

      \[V(s) \leftarrow V(s) + \alpha[\rho_{t:t} R_{t+1} + \rho_{t:t} \gamma V(s') - V(s)],\]

      where $\rho_{t:t} = \frac{\pi(A|S)}{b(A|S)}$

    8. Show that an action-value version of (6.6) holds for the action-value form of the TD error $\delta_t = R_{t+1} + \gamma Q(S_{t+1}, A_{t+1}) - Q(S_t,A_t)$, again assuming that the values don’t change from step to step.

      \[\begin{align} G_t - Q(S_t, A_t) &= R_{t+1} + \gamma G_{t+1} - Q(S_t, A_t) \\ &= R_{t+1} + \gamma G_{t+1} - Q(S_t, A_t) + \gamma Q(S_{t+1}, A_{t+1}) - \gamma Q(S_{t+1}, A_{t+1})\\ &= \delta_t + \gamma(G_{t+1} - Q(S_{t+1}, A_{t+1})) \\ &= \delta_t + \gamma \delta_{t+1} + \gamma^2 (G_{t+2} - Q(S_{t+2}, A_{t+2})) \\ &= \delta_t + \gamma \delta_{t+1} + \gamma^2 \delta_{t+2} + \cdots + \gamma^{T-t-1} \delta_{T-1} + \gamma^{T-t}(G_T - Q(S_T, A_T)) \\ &= \delta_t + \gamma \delta_{t+1} + \gamma^2 \delta_{t+2} + \cdots + \gamma^{T-t-1} \delta_{T-1} + \gamma^{T-t}(0 - 0), \quad G_T, Q(S_T, A_T)\text{ is 0 (terminal state)} \\ &= \sum_{k=t}^{T-1}\gamma^{k-t} \delta_k \end{align}\]

    9. Windy Gridworld with King’s Moves (programming) Re-solve the windy grid world assuming eight possible actions, including the diagonal moves, rather than the usual four. How much better can you do with the extra actions? Can you do even better by including a ninth action that causes no movement at all other than that caused by the wind?

      Code

    10. Stochastic Wind (programming) Re-solve the windy grid world task with King’s moves, assuming that the effect of the wind, if there is any, is stochastic, sometimes varying by 1 from the mean values given for each column. That is, a third of the time you move exactly according to these values, as in the previous exercise, but also a third of the time you move one cell above that, and another third of the time you move one cell below that. For example, if you are one cell to the right of the goal and you move left, then one-third of the time you move one cell above the goal, one-third of the time you move two cells above the goal, and one-third of the time you move to the goal.

      Code

    11. Why is Q-learning considered an off-policy control method?

      The policy for selecting action is different from the policy ($\epsilon$-greedy) for updating the value function (greedy).

    12. Suppose action selection is greedy. Is Q-learning then exactly the same algorithm as Sarsa? Will they make exactly the same action selections and weight updates?

      In this case both algorithm becomes identical. Action Selection and weight updates might differ according to the initialized values. Anyway this willn’t guarantee any convergence because there won’t be any exploration(both algorithms doesn’t explore).

    13. What are the update equations for Double Expected Sarsa with an $\epsilon$-greedy target policy?

      $Q_1(S,A) \leftarrow Q_1(S,A) + \alpha \left[R + \gamma \mathbb{E}[Q_2(S’, A’) | S’] - Q_1(S,A) \right]$

      $Q_2(S,A) \leftarrow Q_2(S,A) + \alpha \left[R + \gamma Q_1(S’, \mathbb{E}[Q_1(S’, A’) | S’]) - Q_2(S,A) \right]$

    14. Describe how the task of Jack’s Car Rental (Example 4.2) could be reformulated in terms of after states. Why, in terms of this specific task, would such are formulation be likely to speed convergence?

      The after-state is number of cars at each location after the car is moved. Convergence becomes more fast because we reduce the number of states.