Balancing the gathering and use of information
Bandits
Multi-armed bandits (MAD) are special case of an RL problem in which the size of the state space and horizon equals one and it has multiple actions, a single state and a greedy horizon.
Regret
The goal of MAB is much similar to that of RL. In RL, the agent maximize the expected cumulative discounted reward. This means the agent maximizes the return through the course of an episode as soon as possibile. But this makes sense only when the environment has multiple states and agents interacts with it for multiple time steps for episode. But MAB has multiple episodes, while only having one single chance to select action in each episode. If we leave the goal to maximize the return, then it wouldnt be straight forward to compare agents. A robust way to capture a more complete goal is to minimize the total expected reward loss while maximizing the expected reward. To calculate this loss, which is called total regret, we sum the per-episode difference of the true expected reward value.
Total regret (\(\tau\)) = \(\sum_{e=1}^E \mathbb{E}[v_* - q_*(A_e)]\)
Approaches to solve MAB environments
There are three major kinds of approaches to tackle a MAB environment.
- Random exploration strategies: This process involves injecting randomness into the action-selection process. ie. agent exploit most of the time, and sometimes it’ll explore using randomness.
- Optimistic exploration strategies: This is a more systematic approach which quantifies the uncertainity in the decision making process and increase the preference for states with highest uncertainity. This helps to explore and face the reality, which lowers the estimate and helps to approach the real value.
- information state-space exploration strategies: These strategies will model the information state of the agent as part of the environment. Encoding the uncertainity as part of the state space means that an environment state will be seen differently when unexplored or explored.
Slippery Bandit Walk
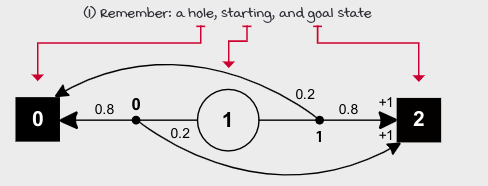
BSW is a grid world with a single row. The leftmost state is a hole and provides 0 reward, while the rightmost state is goal and provides a +1 reward.
In BSW, we get either a 0 or +1 reward. Let’s find out how quickly the agent can figure out an optimal action? and how much total regret will agents accumulate while learning to maximize the expected rewards?
Graph:
Greedy Approach
This is a strategy with exploitation but not exploration. The greedy action-selection or pure exploitation strategy approach consists of always selecting the action with the highest estimated value. There is a chance for the first action to be the best action, but this lucky coincidence decreases as the number of available actions increases.
Pure exploitation in the BSW
- 1st iteration:
-
Agent: The action is the index of the element with the highest value(first element when there are ties).
Q(a) =a = 0 a = 1 0 0 argmax(Q) = 0
-
Environment:
-
- 2nd iteration:
-
Agent:
Q(a) =a = 0 a = 1 1 0 argmax(Q) = 0
-
Environment:

-
- 3rd iteration:
-
Agent:
Q(a) =a = 0 a = 1 0.5 0 argmax(Q) = 0
-
We can see, the agent is already struck with action O. If the Q-table is initialized to zero, and there are no negative rewards in the environment, the greedy strategy will always get stuck with the first action.
pure exploitation strategy
def pure_exploitation(env, n_episodes = 5000):
Q = np.zeros((env.action_space.n))
N = np.zeros((env.action_space.n))
Qe = np.empty((n_episodes, env.action_space.n))
returns = np.empty(n_episodes)
actions = np.empty(n_episodes, dtype=np.int)
name = 'Pure exploitation'
for e in tqdm(range(n_episodes), desc = 'Episodes for:' +name, leave = False):
action = np.argmax(Q)
_, reward, _, _ = env.step(action)
N[action] += 1
Q[action] = Q[action] + (reward - Q[action])/N[action]
Qe[e] = Q
returns[e] = reward
actions[e] = action
return name, returns, Qe, actions
Random Approach
This is a strategy with exploration but not exploitation. And we call this strategy random strategy or a pure exploration strategy. This is simply an approach to action select with no exploitation and sole purpose of this approach is to gain information.
Pure exploration in the BSW
- 1st iteration:
-
Agent: Randomly selects action.
Q(a) =a = 0 a = 1 0 0 random action = 1
-
Environment:

-
- 2nd iteration:
-
Agent: Randomly selects action again.
Q(a) =a = 0 a = 1 0 0 random action = 1
- Environment:

- 3rd iteration:
-
Agent: Randomly selects action with total disregard for the estimates.
Q(a) =a = 0 a = 1 0 0.5 random action = 0 This strategy is not a good one because we don’t want to explore all of the time. Hence we need an algorithm to explore and exploit: gaining and using the information.
-
pure exploration strategy
def pure_exploration(env, n_episodes = 5000):
Q = np.zeros((env.action_space.n))
N = np.zeros((env.action_space.n))
Qe = np.empty((n_episodes, env.action_space.n))
returns = np.empty(n_episodes)
actions = np.empty(n_episodes, dtype=np.int)
name = 'Pure exploration'
for e in tqdm(range(n_episodes), desc = 'Episodes for:' +name, leave = False):
action = np.random.randint(len(Q))
_, reward, _, _ = env.step(action)
N[action] += 1
Q[action] = Q[action] + (reward - Q[action])/N[action]
Qe[e] = Q
returns[e] = reward
actions[e] = action
return name, returns, Qe, actions
Epsilon-greed
This is a combination of pure exploitation and pure exploration, si that agent can exploit and also collect information. This strategy, referred to as the epsilon-greedy strategy, works surprisingly well. Ths will help action-value function to converge to its true value; this will in turn, helps to obtain more rewards in the long term.
Epsilon-greedy in the BSW
- 1st iteration:
-
Agent: Selects action greedily.
Q(a) =a = 0 a = 1 0 0 argmax(Q) = 0
-
Environment:

-
- 2nd iteration:
-
Agent: Randomly selects action again.
Q(a) =a = 0 a = 1 1 0 random action = 1
- Environment:

- 3rd iteration:
-
Agent:
Q(a) =a = 0 a = 1 1 1 random action = 0
-
Epsilon-greedy strategy
def epsilon_greedy(env, epsilon=0.01, n_episodes = 5000):
Q = np.zeros((env.action_space.n))
N = np.zeros((env.action_space.n))
Qe = np.empty((n_episodes, env.action_space.n))
returns = np.empty(n_episodes)
actions = np.empty(n_episodes, dtype=np.int)
name = 'Epsilon-greedy'
for e in tqdm(range(n_episodes), desc = 'Episodes for:' +name, leave = False):
if np.random.random() > epsilon:
action = np.argmax(Q)
else:
action = np.random.randint(len(Q))
_, reward, _, _ = env.step(action)
N[action] += 1
Q[action] = Q[action] + (reward - Q[action])/N[action]
Qe[e] = Q
returns[e] = reward
actions[e] = action
return name, returns, Qe, actions
This strategy is a random exploration strategy because we use randomness to select the action.
Decaying epsilon-greedy
Intutively, early on when the agent hasn’t experienced the environment enough is when we’d like it to explore the mostl while later, as it obtains better estimates of the value functions, we want agent to exploit more. So we start with a high epsilon less than or equal to one, and decay its value on every step. This strategy is called decaying epsilon-greedy strategy.
Linearly decaying Epsilon-greedy strategy
def lin_dec_epsilon_greedy(
env,
init_epsilon=1.0,
min_epsilon = 0.01,
decay_ratio = 0.05,
n_episodes = 5000
):
Q = np.zeros((env.action_space.n))
N = np.zeros((env.action_space.n))
Qe = np.empty((n_episodes, env.action_space.n))
returns = np.empty(n_episodes)
actions = np.empty(n_episodes, dtype=np.int)
name = 'Lin e-greedy {} {} {}'.format(init_epsilon, min_epsilon, decay_ratio)
for e in tqdm(range(n_episodes), desc = 'Episodes for:' +name, leave = False):
decay_episodes = n_episodes * decay_ratio
epsilon = 1 - e/decay_episodes
epsilon *= (init_epsilon - min_epsilon)
epsilon += min_epsilon
epsilon = np.clip(epsilon, min_epsilon, init_epsilon)
if np.random.random() > epsilon:
action = np.argmax(Q)
else:
action = np.random.randint(len(Q))
_, reward, _, _ = env.step(action)
N[action] += 1
Q[action] = Q[action] + (reward - Q[action])/N[action]
Qe[e] = Q
returns[e] = reward
actions[e] = action
return name, returns, Qe, actions
Exponentially decaying Epsilon-greedy strategy
def exp_dec_epsilon_greedy(
env,
init_epsilon=1.0,
min_epsilon = 0.01,
decay_ratio = 0.05,
n_episodes = 5000
):
Q = np.zeros((env.action_space.n))
N = np.zeros((env.action_space.n))
Qe = np.empty((n_episodes, env.action_space.n))
returns = np.empty(n_episodes)
actions = np.empty(n_episodes, dtype=np.int)
decay_episodes = int(n_episodes*decay_ratio)
rem_episodes = n_episodes - decay_episodes
epsilons = 0.01
epsilons /= np.logspace(-2, 0, decay_episodes)
epsilons *= init_epsilon - min_epsilon
epsilons += min_epsilon
epsilons = np.pad(epsilons, (0, rem_episodes), 'edge')
name = 'Lin e-greedy {} {} {}'.format(init_epsilon, min_epsilon, decay_ratio)
for e in tqdm(range(n_episodes), desc = 'Episodes for:' +name, leave = False):
if np.random.random() > epsilons[e]:
action = np.argmax(Q)
else:
action = np.random.randint(len(Q))
_, reward, _, _ = env.step(action)
N[action] += 1
Q[action] = Q[action] + (reward - Q[action])/N[action]
Qe[e] = Q
returns[e] = reward
actions[e] = action
return name, returns, Qe, actions
Optimistic Initialization
This is an approach in which treating actions that haven’t sufficiently been explored as the best possible action. This class of strategies is known as optimism in the face of uncertainity. The mechanism of this strategy is pretty straightforward: we initialize the Q-function to a high value and act greedily using these estimates. In addition to the Q-value we will also need counts which is higher than one. If we don’t, the Q-function will change quickly, and effect will be reduced.
Optimistic Initialization in the BSW
Initial Q = 1, count = 10
- 1st iteration:
-
Agent: Selects action greedily.
Q(a) =a = 0 a = 1 1 1 argmax(Q) = 0
-
Environment:

The environment gets a zero reward.
-
- 2nd iteration:
-
Agent: Greedily selects action 1. 0.91 is because 10/11 ie. total reward by counts.
Q(a) =a = 0 a = 1 0.91 1 argmax(Q) = 1
-
Environment:

-
- 3rd iteration:
-
Agent:
Q(a) =a = 0 a = 1 0.91 0.91 argmax(Q) = 0
-
Q-values continues getting lower and lower as they converge to the optimal.
Optimistic Initialization strategy
def Optimistic_Initialization(
env,
Optimistic_estimate = 0.1,
initial_count = 100,
n_episodes = 5000
):
Q = np.full(
(env.action_space.n),
Optimistic_estimate, dtype=np.float64)
N = np.full(
(n_episodes, env.action_space.n),
Optimistic_estimate, dtype=np.float64)
Qe = np.empty((n_episodes, env.action_space.n))
returns = np.empty(n_episodes)
actions = np.empty(n_episodes, dtype=np.int)
name = 'Optimistic {} {}'.format(Optimistic_estimate, initial_count)
for e in tqdm(range(n_episodes), desc = 'Episodes for:' +name, leave = False):
action = np.argmax(Q)
_, reward, _, _ = env.step(action)
N[action] += 1
Q[action] = Q[action] + (reward - Q[action])/N[action]
Qe[e] = Q
returns[e] = reward
actions[e] = action
return name, returns, Qe, actions
Strategic exploration
Softmax
Random exploration strategy makes more sense if they take into account Q-value estimates. By doing so, its less likely to select an action with low estimate. We use Softmax to try this approach. It samples an action from a probability distribution over the action-value function such that the probability of selecting an action is proportional to its current action-value estimate.
To select the action at episode e
\[\begin{align*} A_e = \underset{a}{argmax} \left[Q_e(a) + c \sqrt{\frac{\ln e}{N_e(a)}} \right] \end{align*} \\\]Softmax strategy
def softmax(
env,
init_temp = 1000.0,
min_temp = 0.1,
decay_ratio = 0.04,
n_episodes = 5000
):
Q = np.zeros((env.action_space.n))
N = np.zeros((env.action_space.n))
Qe = np.empty((n_episodes, env.action_space.n))
returns = np.empty(n_episodes)
actions = np.empty(n_episodes, dtype=np.int)
name = 'Softmax {} {} {}'.format(init_temp, min_temp, decay_ratio)
for e in tqdm(
range(n_episodes),
desc = 'Episodes for:' + name,
leave = False
):
decay_episodes = n_episodes * decay_ratio
temp = 1 - e / decay_episodes
temp *= init_temp - min_temp
temp += min_temp
temp = np.clip(temp, min_temp, init_temp)
Scaled_Q = Q / temp
norm_Q = Scaled_Q - np.max(Scaled_Q)
exp_Q = np.exp(norm_Q)
probs = exp_Q / np.sum(exp_Q)
assert np.isclose(np.sum(probs), 1.0)
action = np.random.choice(
np.arange(len(probs)), size=1, p=probs
)[0]
_, reward, _, _ = env.step(action)
N[action] += 1
Q[action] = Q[action] + (reward - Q[action])/N[action]
Qe[e] = Q
returns[e] = reward
actions[e] = action
return name, returns, Qe, actions
UCB: Upper confidence bound
In UCB, we’re Optimistic but more of realistic optimism; instead of blindly hoping for the best. Themore uncertain a Q-value estimate the more critical it is to explore it.
To select an action at episode e,
\[\begin{align*} A_e = \underset{a}{argmax} \left[ Q_e(a) + c \sqrt{\frac{\ln e}{N_e(a)}}\right] \end{align*} \\\]Upper Confidence Bound
def upper_confidence_bound(
env,
c = 2,
n_episodes = 5000
):
Q = np.zeros((env.action_space.n))
N = np.zeros((env.action_space.n))
Qe = np.empty((n_episodes, env.action_space.n))
returns = np.empty(n_episodes)
actions = np.empty(n_episodes, dtype=np.int)
name = 'UCB {}'.format(c)
for e in tqdm(
range(n_episodes),
desc = 'Episodes for:' + name,
leave = False
):
if e < len(Q):
action = e
else:
U = c*np.sqrt(np.log(e)/ N)
action = np.argmax(U+Q)
_, reward, _, _ = env.step(action)
N[action] += 1
Q[action] = Q[action] + (reward - Q[action])/N[action]
Qe[e] = Q
returns[e] = reward
actions[e] = action
return name, returns, Qe, actions
Thompson sampling
The UCB algorithm is a frequentist apporach to dealing with the exploration versus exploitation trade-off because it makes minimal assumptions about the distribution underlying the Q function. But other techniques, such as Bayseian strategies, can use priors to make reasonable assumptions and exploit this knowledge. The thompson sampling strategy is a sample based probability matching strategy that allows us to use Bayseian techniques to balance exploration and exploitation. A simple way to implement this strategy is by keeping each Q-value guassian distribution.
Thompson Sampling Strategy
def thompson_sampling(env, alpha=1, beta=0, n_episodes=5000):
Q = np.zeros((env.action_space.n))
N = np.zeros((env.action_space.n))
Qe = np.empty((n_episodes, env.action_space.n))
returns = np.empty(n_episodes)
actions = np.empty(n_episodes, dtype=np.int)
name = f"Thompson Sampling: {alpha} {beta}"
for e in tqdm(range(n_episodes), desc="Episodes for:" + name, leave=False):
samples = np.random.normal(loc=Q, scale=alpha / (np.sqrt(N) + beta))
action = np.argmax(samples)
_, reward, _, _ = env.step(action)
N[action] += 1
Q[action] = Q[action] + (reward - Q[action]) / N[action]
Qe[e] = Q
returns[e] = reward
actions[e] = action
return name, returns, Qe, actions